题目内容
14.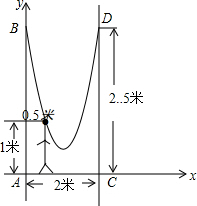 如图,小明的父亲在相距2米的两棵树(AB、CD)间拴了一根绳子,给小明做了一个简易的秋千.拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子.以A为原点,AC所在直线为x轴,AB所在直线为y轴,建立如图所示的直角坐标系.
如图,小明的父亲在相距2米的两棵树(AB、CD)间拴了一根绳子,给小明做了一个简易的秋千.拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子.以A为原点,AC所在直线为x轴,AB所在直线为y轴,建立如图所示的直角坐标系.(1)求此抛物线的表达式;
(2)求绳子的最低点距地面的距离.
分析 (1)根据题意建立直角坐标系,点(0,2.5)、(2,2.5)、(0.5,1)都在抛物线上,设抛物线解析式,列方程组,求解析式.
(2)根据(1)的解析式很容易就可求出抛物线的顶点坐标,纵坐标的绝对值即为绳子的最低点距地面的距离.
解答 解:(1)按要求建立直角坐标系.
设抛物线的函数关系式为:y=ax2+bx+c.
将(0,2.5)、(2,2.5)、(0.5,1)代入y=ax2+bx+c得:
$\left\{\begin{array}{l}{c=2.5}\\{4a+2b+c=2.5}\\{\frac{1}{4}a+\frac{1}{2}b+c=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=2}\\{b=-4}\\{c=2.5}\end{array}\right.$.
∴抛物线的表达式为:y=2x2-4x+2.5;
(2)y=2x2-4x+2.5=2(x-1)2+0.5
∵抛物线的顶点坐标为(1,0.5),
∴绳子的最低点距地面的距离为0.5m.
点评 本题主要考查函数解析式和点的坐标的求法,借助二次函数解决实际为题,本题关键在于正确选择原点建立直角坐标系,正确确定有关点的坐标,求出抛物线解析式.

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案
相关题目
18.下列各式能用加法运算律简化计算的是( )
| A. | 3$\frac{1}{2}$+(-2$\frac{1}{3}$) | B. | 6$\frac{2}{5}$+$\frac{1}{2}$+3 | ||
| C. | (-8)+(-7.8)+(-2)+(+6.8) | D. | 4$\frac{1}{2}$+(-$\frac{8}{7}$)+(-3$\frac{1}{3}$)+(-2$\frac{1}{5}$) |
19.设x1,x2是一元二次方程x2+2x-1=0的两个限,则2x12+5x1+x2的值为( )
| A. | 2 | B. | 1 | C. | 0 | D. | -1 |
4.如果代数式$\frac{3-2x}{2}$与$\frac{2-x}{3}$的值互为相反数,则x应为( )
| A. | -$\frac{13}{8}$ | B. | $\frac{13}{8}$ | C. | -2 | D. | 2 |

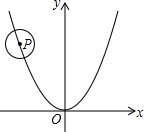 如图,已知⊙P的半径为2,圆心P在抛物线y=x2-2上运动,当⊙P与x轴相切时,圆心P的坐标为(2,2)或(-2,2).
如图,已知⊙P的半径为2,圆心P在抛物线y=x2-2上运动,当⊙P与x轴相切时,圆心P的坐标为(2,2)或(-2,2).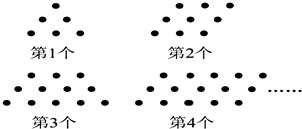 用同样大小的黑色棋子按如图的规律摆放:
用同样大小的黑色棋子按如图的规律摆放:
 如图,在△ABC中,点Q,M在BC上,点P,N分别在AB,AC上,边BC=120毫米,高AD=80毫米,四边形PQMN为矩形,设△ABC的高AD与PN相交于点E.
如图,在△ABC中,点Q,M在BC上,点P,N分别在AB,AC上,边BC=120毫米,高AD=80毫米,四边形PQMN为矩形,设△ABC的高AD与PN相交于点E.