题目内容
4.已知二次函数y=a(x-2)2+3的图象经过点(-1,0).(1)求这个二次函数的解析式;
(2)分别指出这个二次函数图象的开口方向、对称轴和顶点坐标.
分析 (1)把(-1,0)代入二次函数解析式求出a的值,即可确定出解析式;
(2)利用二次根式的性质确定出开口方向,顶点坐标以及对称轴即可.
解答 解:(1)把(-1,0)代入二次函数解析式得:9a+3=0,即a=-$\frac{1}{3}$,
则函数解析式为y=-$\frac{1}{3}$(x-2)2+3;
(2)∵a=-$\frac{1}{3}$<0,
∴抛物线开口向下,
顶点坐标为(2,3),对称轴为直线x=2.
点评 此题考查了待定系数法求二次函数解析式,以及二次函数的性质,熟练掌握待定系数法是解本题的关键.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
19.设x1,x2是一元二次方程x2+2x-1=0的两个限,则2x12+5x1+x2的值为( )
| A. | 2 | B. | 1 | C. | 0 | D. | -1 |
 如图所示,已知△ABE≌△ACD.
如图所示,已知△ABE≌△ACD.
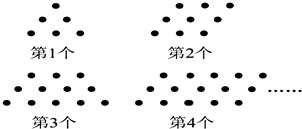 用同样大小的黑色棋子按如图的规律摆放:
用同样大小的黑色棋子按如图的规律摆放: