题目内容
16. 已知菱形ABCD的两条对角线分别是6和8,求:
已知菱形ABCD的两条对角线分别是6和8,求:(1)菱形的边长;
(2)菱形的面积;
(3)菱形的高.
分析 (1)由菱形的性质得出AB=BC=CD=DA,AO=$\frac{1}{2}$AC=3,BO=$\frac{1}{2}$BD=4,AC⊥BD,由勾股定理求出AB即可;
(2)菱形的面积等于两条对角线长的积的一半,即可得出结果;
(3)作AE⊥CD于E,由菱形ABCD的面积S=AB•AE,求出AE即可.
解答 解:(1)∵四边形ABCD是菱形,
∴AB=BC=CD=DA,AO=$\frac{1}{2}$AC=3,BO=$\frac{1}{2}$BD=4,AC⊥BD,
∴∠AOB=90°,
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
即菱形的边长为5;
(2)∵AC⊥BD,
∴菱形ABCD的面积S=$\frac{1}{2}$AC×BD=$\frac{1}{2}$×6×8=24;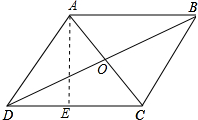
(3)作AE⊥CD于E,如图所示:
∵菱形ABCD的面积S=AB•AE=24,
∴AE=$\frac{24}{5}$;
即菱形的高为$\frac{24}{5}$.
点评 本题考查了菱形的性质、菱形面积的计算、勾股定理;熟练掌握菱形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
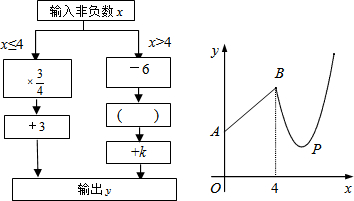
4.如图是数值转换机的示意图,小明按照其对应系画出了y与x的函数图象.
(1)分别写出当0≤x≤4与x>4时,y与x的函数关系式;
(2)求出所有输出y的值的最小数值;
(3)当输出y的值为3时,求x的值.
(1)分别写出当0≤x≤4与x>4时,y与x的函数关系式;
(2)求出所有输出y的值的最小数值;
(3)当输出y的值为3时,求x的值.

1.已知a<-1,点(a-1,y1),(a,y2),(a+1,y3)都在函数y=x2+1的图象上,则( )
| A. | y1<y2<y3 | B. | y1<y3<y2 | C. | y3<y2<y1 | D. | y2<y1<y3 |
 如图,P为正方形ABCD边CD上一点,∠BAP的平分线交BC于点Q,说明:AP=DP+BQ.
如图,P为正方形ABCD边CD上一点,∠BAP的平分线交BC于点Q,说明:AP=DP+BQ. 如图所示,山坡AB的坡度为5:12,一辆汽车从山脚A处出发,把货物运到高度为75m的山顶B处,求汽车从A到B所行驶的路程.
如图所示,山坡AB的坡度为5:12,一辆汽车从山脚A处出发,把货物运到高度为75m的山顶B处,求汽车从A到B所行驶的路程. 如图,两圆轮叠靠在墙边,已知两轮半径分别为1和4,它们与墙的切点为A,B,则小圆轮上最高点与地面间的距离为9.
如图,两圆轮叠靠在墙边,已知两轮半径分别为1和4,它们与墙的切点为A,B,则小圆轮上最高点与地面间的距离为9.