题目内容
5．
如图，两圆轮叠靠在墙边，已知两轮半径分别为1和4，它们与墙的切点为A，B，则小圆轮上最高点与地面间的距离为9．
分析 连接圆心CD，AC、BD，作CE⊥BD于E，根据矩形的判定定理得到BE=AC=1，根据外切两圆的性质求出CD的长，根据勾股定理求出CE的长，得到答案．
解答 解：
连接圆心CD，AC、BD，作CE⊥BD于E，
则四边形ABEC为矩形，
∴BE=AC=1，
∴DE=BD-BE=3，又CD=1+4=5，
由勾股定理得，CE=4，
∴小圆轮上最高点与地面间的距离为1+4+4=9，
故答案为：9．
点评 本题考查的是相切两圆的性质和勾股定理的应用，掌握外切两圆的圆心距等于两圆半径之和是解题的关键．
练习册系列答案
相关题目
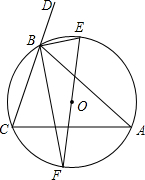如图，已知BF、BE分别是△ABC的内角∠ABC与外角∠ABD的平分线，BF、BE分别与△ABC的外接圆O交于点F、E．求证：
已知菱形ABCD的两条对角线分别是6和8，求：
已知：如图，在四边形ABCD中，AB=CD，∠BAC=∠ACD，求证：△ABC≌△CDA．
如图，以AD为边的三角形是△ABD，△ADC，以∠B为内角的三角形是△ABD，△ABC，△ACD的三个内角分别是∠ACD，∠ADC，∠CAD；三边分别是AC，AD，CD．
10．如图，在下面四个物体中，最接近圆柱的是（ ）
| A． |  烟筒 | B． |  弯管 | C． |  玩具硬币 | D． |  某种饮料瓶 |
已知：关于x的一元二次方程mx2-（3m+2）x+2m+2=0（m＞0）．
．