题目内容
2.已知m为整数且-1<m<2$\sqrt{5}$,若$\sqrt{m+1}$为整数,则m=0或3.分析 先求出2$\sqrt{5}$=$\sqrt{20}$的范围,根据不等式组求出整数m的值,再根据$\sqrt{m+1}$为整数求出即可.
解答 解:∵-1<m<2$\sqrt{5}$,4<2$\sqrt{5}$=$\sqrt{20}$<5,
∴m的整数值为0,1,2,3,4,
∵$\sqrt{m+1}$为整数,
∴m只能为0或3,
故答案为:0或3.
点评 本题考查了估算无理数的大小,二次根式的性质,不等式组的应用,解此题的关键算式求出2$\sqrt{5}$=$\sqrt{20}$的范围,注意:$\sqrt{m+1}$为整数的条件是m+1是一个完全平方数.

练习册系列答案
相关题目
12. 如图,在数学课上,老师用5个完全相同的小长方形的无重叠的情况下拼成了一个大长方形,已知小长方形的长为3$\sqrt{10}$、宽为2$\sqrt{10}$,下列是四位同学对该大长方形的判断,其中不正确的是( )
如图,在数学课上,老师用5个完全相同的小长方形的无重叠的情况下拼成了一个大长方形,已知小长方形的长为3$\sqrt{10}$、宽为2$\sqrt{10}$,下列是四位同学对该大长方形的判断,其中不正确的是( )
 如图,在数学课上,老师用5个完全相同的小长方形的无重叠的情况下拼成了一个大长方形,已知小长方形的长为3$\sqrt{10}$、宽为2$\sqrt{10}$,下列是四位同学对该大长方形的判断,其中不正确的是( )
如图,在数学课上,老师用5个完全相同的小长方形的无重叠的情况下拼成了一个大长方形,已知小长方形的长为3$\sqrt{10}$、宽为2$\sqrt{10}$,下列是四位同学对该大长方形的判断,其中不正确的是( )| A. | 大长方形的长为6$\sqrt{10}$ | B. | 大长方形的宽为5$\sqrt{10}$ | ||
| C. | 大长方形的长为11$\sqrt{10}$ | D. | 大长方形的面积为300 |
7.下列个数中,不是无理数的是( )
| A. | 0.$\stackrel{.}{5}$ | B. | $\sqrt{7}$ | C. | π | D. | 0.151151115… |
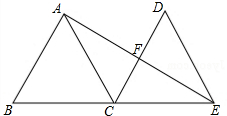 如图,等边△ABC的边长为6,现将△ABC沿直线向右平移,使点B与点C重合,得△DCE,连结AE交DC于点F.
如图,等边△ABC的边长为6,现将△ABC沿直线向右平移,使点B与点C重合,得△DCE,连结AE交DC于点F.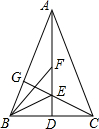 如图,△ABC中,AB=AC,AD⊥BC于点D,射线BE、BF将∠ABC三等分交AD于E、F两点,连接CE并延长交AB于点G,求证:$\frac{AF}{EF}$=$\frac{AG}{GB}$.
如图,△ABC中,AB=AC,AD⊥BC于点D,射线BE、BF将∠ABC三等分交AD于E、F两点,连接CE并延长交AB于点G,求证:$\frac{AF}{EF}$=$\frac{AG}{GB}$.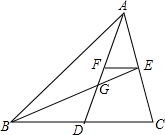 如图,点G为△ABC的重心,连接AG、BG并延长,分别交BC、AC于点D、E,过点E作EF∥BC交AD于点F,那么$\frac{FG}{AG}$=$\frac{1}{4}$.
如图,点G为△ABC的重心,连接AG、BG并延长,分别交BC、AC于点D、E,过点E作EF∥BC交AD于点F,那么$\frac{FG}{AG}$=$\frac{1}{4}$.