题目内容
15.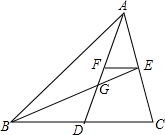 如图,点G为△ABC的重心,连接AG、BG并延长,分别交BC、AC于点D、E,过点E作EF∥BC交AD于点F,那么$\frac{FG}{AG}$=$\frac{1}{4}$.
如图,点G为△ABC的重心,连接AG、BG并延长,分别交BC、AC于点D、E,过点E作EF∥BC交AD于点F,那么$\frac{FG}{AG}$=$\frac{1}{4}$.
分析 由三角形的重心定理得出,$\frac{EG}{BG}$=$\frac{1}{2}$,$\frac{DG}{AG}$=$\frac{1}{2}$,由平行线分线段成比例定理得出$\frac{FG}{DG}$=$\frac{EG}{BG}$=$\frac{1}{2}$,即可得出结果.
解答 解:∵点G为△ABC的重心,
∴$\frac{EG}{BG}$=$\frac{1}{2}$,$\frac{DG}{AG}$=$\frac{1}{2}$,
∵EF∥BC,$\frac{FG}{DG}$=$\frac{EG}{BG}$=$\frac{1}{2}$,
∴$\frac{FG}{AG}$=$\frac{1}{4}$,
故答案为:$\frac{1}{4}$.
点评 本题考查了平行线分线段成比例定理、三角形的重心定理;熟练掌握三角形的重心定理,由平行线分线段成比例定理得出FG:DG=1:2是解决问题的关键.

练习册系列答案
相关题目
3.使不等式x>-$\frac{7}{3}$且x<2同时成立的所有整数的和是( )
| A. | 0 | B. | 1 | C. | -2 | D. | -1 |
20.若等式$\sqrt{(x-2)(x+1)}$=$\sqrt{x-2}$$•\sqrt{x+1}$成立,则x的取值范围是( )
| A. | x≥2 | B. | x≥1 | C. | -1≤x≤2 | D. | x≤-1或x≥2 |
7.3210000用科学记数法表示应为( )
| A. | 0.321×107 | B. | 321×104 | C. | 3.21×106 | D. | 3.21×105 |
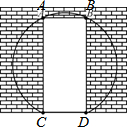 如图,一面墙上有一个矩形的门洞,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接矩形,已知矩形的高AC=2米,宽CD=$\frac{2}{3}\sqrt{3}$米.
如图,一面墙上有一个矩形的门洞,现要将它改为一个圆弧形的门洞,圆弧所在的圆外接矩形,已知矩形的高AC=2米,宽CD=$\frac{2}{3}\sqrt{3}$米.