题目内容
10.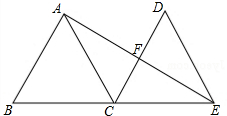 如图,等边△ABC的边长为6,现将△ABC沿直线向右平移,使点B与点C重合,得△DCE,连结AE交DC于点F.
如图,等边△ABC的边长为6,现将△ABC沿直线向右平移,使点B与点C重合,得△DCE,连结AE交DC于点F.(1)猜想AE与CD的位置,并证明你的结论;
(2)求AE的长.
分析 (1)由平移的性质可知AC=CE,再证明CF平分∠ACE即可得出结论;
(2)在Rt△ABE中利用勾股定理即可得出AE的长.
解答 解:(1)AE⊥CD.
∵△DCE由△ABC平移而成,
∴AC=CE=6,∠ACB=∠DCE=60°,
∴∠ACF=∠DCE=60°,
∴AE⊥CD,
(2)∵由(1)知,AB∥CD,CD⊥AE,
∴△BAE是直角三角形,
∵AB=6,BE=2AE=12,
∴AE=$\sqrt{B{E}^{2}-A{B}^{2}}$=6$\sqrt{3}$.
点评 本题考查的是等边三角形的性质及平移的性质,熟知图形平移后的图形与原图形全等的性质是解答此题的关键.

练习册系列答案
相关题目
20.下列窗花图案中是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
3.使不等式x>-$\frac{7}{3}$且x<2同时成立的所有整数的和是( )
| A. | 0 | B. | 1 | C. | -2 | D. | -1 |
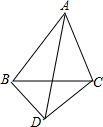 在△ABC中,AB=3,∠BAC=60°,把线段BC绕C点逆时针旋转得到线段CD,∠ACB+∠ACD=180°,AD=$\sqrt{19}$,则线段BC的长度为$\frac{\sqrt{31}}{2}$.
在△ABC中,AB=3,∠BAC=60°,把线段BC绕C点逆时针旋转得到线段CD,∠ACB+∠ACD=180°,AD=$\sqrt{19}$,则线段BC的长度为$\frac{\sqrt{31}}{2}$.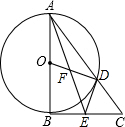 如图,在△ABC中,∠ABC=90°,以AB为直径作⊙O交AC于点D,E是BC的中点,连接AE、OD、DE、AE与OD相交于F.
如图,在△ABC中,∠ABC=90°,以AB为直径作⊙O交AC于点D,E是BC的中点,连接AE、OD、DE、AE与OD相交于F.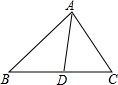 如图,△ABC,AD平分∠BAC交BC于点D,求证:$\frac{BD}{CD}$=$\frac{AB}{AC}$.
如图,△ABC,AD平分∠BAC交BC于点D,求证:$\frac{BD}{CD}$=$\frac{AB}{AC}$.