题目内容
14.已知x=$\sqrt{\frac{2-\sqrt{3}}{2}}$,则4x2+4x-2017=-2015.分析 先对式子4x2+4x-2017进行化简变为完全平方式,然后代入求值即可解答本题.
解答 解:∵x=$\sqrt{\frac{2-\sqrt{3}}{2}}$,
∴4x2+4x-2017
=(2x+1)2-2018
=$(2×\sqrt{\frac{2-\sqrt{3}}{2}}+1)^{2}-2018$
=$(\sqrt{4-2\sqrt{3}}+1)^{2}-2018$
=$(\sqrt{3}-1+1)^{2}-2018$
=3-2018
=-2015.
故答案为;-2015.
点评 本题考查二次根式的化简求值,解题的关键是巧妙的对原式进行变形,然后进行求值即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.使不等式x>-$\frac{7}{3}$且x<2同时成立的所有整数的和是( )
| A. | 0 | B. | 1 | C. | -2 | D. | -1 |
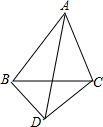 在△ABC中,AB=3,∠BAC=60°,把线段BC绕C点逆时针旋转得到线段CD,∠ACB+∠ACD=180°,AD=$\sqrt{19}$,则线段BC的长度为$\frac{\sqrt{31}}{2}$.
在△ABC中,AB=3,∠BAC=60°,把线段BC绕C点逆时针旋转得到线段CD,∠ACB+∠ACD=180°,AD=$\sqrt{19}$,则线段BC的长度为$\frac{\sqrt{31}}{2}$.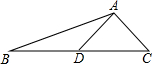 如图,AD是△ABC的中线,tanB=$\frac{1}{3}$,cosC=$\frac{\sqrt{2}}{2}$,AC=$\sqrt{2}$.求:
如图,AD是△ABC的中线,tanB=$\frac{1}{3}$,cosC=$\frac{\sqrt{2}}{2}$,AC=$\sqrt{2}$.求: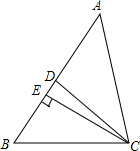 如图,在△ABC中,CD是∠ACB的角平分线,CE是AB边上的高,若∠DCE=10°,∠B=60°,求∠A的度数.
如图,在△ABC中,CD是∠ACB的角平分线,CE是AB边上的高,若∠DCE=10°,∠B=60°,求∠A的度数.