题目内容
13.将一张面积为400cm2的正方形纸片,沿着平行于边的方向剪出一块长方形纸片,甲的方案是:长方形的面积是300cm2,且长与宽的比为3:2,乙的方案是:长方形的面积为150cm2,且长与宽的比是5:3,问甲、乙两人的方案是否可行?并说明理由.分析 在甲方案中可设它的长为3x,则它的宽为2x,根据面积公式列出一元二次方程解答即可求出x的值,再代入长宽的表达式,看是否符合条件即可判断,同理可判断乙方案是否可行.
解答 解:甲的方案不可行,乙方案可行.
甲方案中,设长方形纸片的长为3xcm,宽为2xcm,
则3x•2x=300,即6x2=300,x2=50,
解得:x=5$\sqrt{2}$
∴长方形的长为15$\sqrt{2}$cm.
∵15$\sqrt{2}$>20,
但正方形纸片的边长只有20cm;
乙方案中,设长方形纸片的长为5xcm,宽为3xcm,
则3x•5x=150,即15x2=150,
解得:x=$\sqrt{10}$,
∴长方形的长为5$\sqrt{10}$<20,
故乙方案可行,
综上,甲方案不可行,乙方案可行.
点评 本题考查了一元二次方程的应用以及算术平方根和正方形性质等知识,解题的关键是先求出所裁出的长方形纸片的长结合题意去判断.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
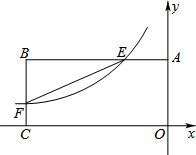 如图,反比例函数$y=\frac{k}{x}$(k<0)的图象与矩形OABC的边相交于E、F两点,连接EF,且BE=2AE,点E坐标为(-2,3).
如图,反比例函数$y=\frac{k}{x}$(k<0)的图象与矩形OABC的边相交于E、F两点,连接EF,且BE=2AE,点E坐标为(-2,3).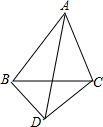 在△ABC中,AB=3,∠BAC=60°,把线段BC绕C点逆时针旋转得到线段CD,∠ACB+∠ACD=180°,AD=$\sqrt{19}$,则线段BC的长度为$\frac{\sqrt{31}}{2}$.
在△ABC中,AB=3,∠BAC=60°,把线段BC绕C点逆时针旋转得到线段CD,∠ACB+∠ACD=180°,AD=$\sqrt{19}$,则线段BC的长度为$\frac{\sqrt{31}}{2}$.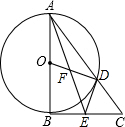 如图,在△ABC中,∠ABC=90°,以AB为直径作⊙O交AC于点D,E是BC的中点,连接AE、OD、DE、AE与OD相交于F.
如图,在△ABC中,∠ABC=90°,以AB为直径作⊙O交AC于点D,E是BC的中点,连接AE、OD、DE、AE与OD相交于F.