题目内容
16.若关于x的方程(x-2)|x|-k=0有三个不相等的实数根,则实数k的取值范围是-1<k<0.分析 由方程(x-2)|x|-k=0得k=(x-2)|x|,然后利用分段函数,作出函数的图象,利用图象确定k的取值范围即可.
解答 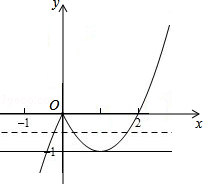 解:由(x-2)|x|-k=0得k=(x-2)|x|,设f(x)=(x-2)|x|,则f(x)=$\left\{\begin{array}{l}{(x-2)x,x≥0}\\{-(x-2)x,x<0}\end{array}\right.$,
解:由(x-2)|x|-k=0得k=(x-2)|x|,设f(x)=(x-2)|x|,则f(x)=$\left\{\begin{array}{l}{(x-2)x,x≥0}\\{-(x-2)x,x<0}\end{array}\right.$,
作出函数f(x)的图象如图:
由图象知要使方程(x-2)|x|-k=0有三个不相等的实根,则-1<k<0.
故k的取值范围是:-1<k<0.
故答案为:-1<k<0.
点评 本题主要考查函数与方程的应用,利用数形结合是解决此类问题的基本方法.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
7.用圆心角为120°,半径为6 cm的扇形纸片卷成一个圆锥形无底纸帽(如图所示),则这个纸帽的底面周长是( )
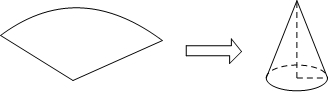

| A. | 2π cm | B. | 3π cm | C. | 4π cm | D. | 5π cm |
11. 某一小球以一定的初速度开始向前滚动,并且均匀减速,小球滚动的速度v(单位:米/秒)与时间x(单位:秒)之间关系的部分数据如表一:
某一小球以一定的初速度开始向前滚动,并且均匀减速,小球滚动的速度v(单位:米/秒)与时间x(单位:秒)之间关系的部分数据如表一:
表一:
(1)根据表一的信息,请在表二中填写滚动的距离s(单位:米)的对应值,(提示:本题中,s=$\overline{v}$×x,$\overline{v}$=$\frac{{v}_{0}+{v}_{x}}{2}$,其中,v0表示开始时的速度,vx表示x秒时的速度.)
表二:
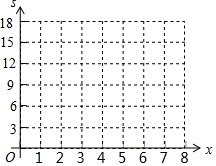
(2)根据表二中的数据在给出的平面坐标系中画出相应的点;
(3)选择适当的函数表示s与x之间的关系,求出相应的函数解析式;
(4)当s=13.75时,求滚动时间x.
 某一小球以一定的初速度开始向前滚动,并且均匀减速,小球滚动的速度v(单位:米/秒)与时间x(单位:秒)之间关系的部分数据如表一:
某一小球以一定的初速度开始向前滚动,并且均匀减速,小球滚动的速度v(单位:米/秒)与时间x(单位:秒)之间关系的部分数据如表一:表一:
| 时间x(秒) | 0 | 1 | 2 | 2.5 | 3 | … |
| 速度v(米/秒) | 8 | 6 | 4 | 3 | 2 | … |
表二:
| 时间x(秒) | 0 | 1 | 2 | 3 | … |
| 距离s(米) | 0 | … |
(3)选择适当的函数表示s与x之间的关系,求出相应的函数解析式;
(4)当s=13.75时,求滚动时间x.
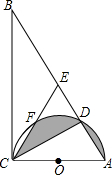 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AB=12,以AC为直径的半圆O交AB于点D,点E是AB的中点,CE交半圆O于点F,求图中阴影部分的面积.
如图,在Rt△ABC中,∠ACB=90°,∠B=30°,AB=12,以AC为直径的半圆O交AB于点D,点E是AB的中点,CE交半圆O于点F,求图中阴影部分的面积.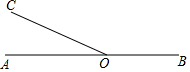 在直线AB上任取一点O,过点O作射线OC、OD,使OC⊥OD,如果∠AOC=30°,OE平分∠BOD,求∠COE(要求:将图形补充完整,写出求解过程)
在直线AB上任取一点O,过点O作射线OC、OD,使OC⊥OD,如果∠AOC=30°,OE平分∠BOD,求∠COE(要求:将图形补充完整,写出求解过程)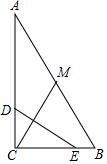 如图,在Rt△ABC中,点D、E分别在AC、BC上,将△CDE沿直线DE翻折,点C恰好落在斜边AB的中点M处.
如图,在Rt△ABC中,点D、E分别在AC、BC上,将△CDE沿直线DE翻折,点C恰好落在斜边AB的中点M处. 某长方体包装盒的表面积为146cm2,其展开图如图所示.求这个包装盒的体积.
某长方体包装盒的表面积为146cm2,其展开图如图所示.求这个包装盒的体积.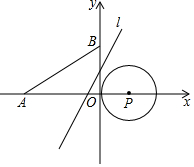 如图,平面直角坐标系中,点P的坐标为(1,0),⊙P的半径为1,点A的坐标为(-3,0),点B在y轴的正半轴上,且OB=$\sqrt{3}$.若直线1:y=$\sqrt{3}$x+m从点B开始沿y轴向下平移,线段AB与线段A′B′关于直线1对称.若线段A′B′与⊙P只有一个公共点,则m的值为$\sqrt{3}$或-$\frac{\sqrt{3}}{3}$.
如图,平面直角坐标系中,点P的坐标为(1,0),⊙P的半径为1,点A的坐标为(-3,0),点B在y轴的正半轴上,且OB=$\sqrt{3}$.若直线1:y=$\sqrt{3}$x+m从点B开始沿y轴向下平移,线段AB与线段A′B′关于直线1对称.若线段A′B′与⊙P只有一个公共点,则m的值为$\sqrt{3}$或-$\frac{\sqrt{3}}{3}$.