Question

6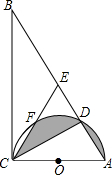．如图，在Rt△ABC中，∠ACB=90°，∠B=30°，AB=12，以AC为直径的半圆O交AB于点D，点E是AB的中点，CE交半圆O于点F，求图中阴影部分的面积．

Answer 1

分析 易证∠BCE=∠ACD，则根据弦切角定理可以得到 $\widehat{AD}$与弦AD围成的弓形的面积等于 $\widehat{CF}$与弦CF围成的弓形的面积相等，则阴影部分的面积等于半圆的面积减去直角△ACD的面积，再减去弓形的面积，据此即可求解．

解答 解：∵Rt△ABC中，∠ACB=90°，∠B=30°，AB=12cm，
∴AC=$\frac{1}{2}$AB=6cm，∠A=60°
∵E是AB的中点，
∴CE=$\frac{1}{2}$AB，
则△ACE是等边三角形．
∴∠BCE=90°-60°=30°，
∵AC是直径，
∴∠CDA=90°，
∴∠ACD=90°-∠A=30°，
∴∠BCE=∠ACD，
∴$\widehat{CF}$=$\widehat{AD}$=，
连接OD，作OG⊥CD于点G，
则∠COD=120°，OG=$\frac{1}{2}$OC=$\frac{3}{2}$，CG=$\frac{1}{2}$CD=$\frac{3\sqrt{3}}{2}$．
∴阴影部分的面积为：S_扇形COD-S_△COD=$\frac{120π•{3}^{2}}{360}$-$\frac{1}{2}$×$\frac{3}{2}$×3 $\sqrt{3}$=3π-$\frac{9\sqrt{3}}{4}$．

点评 本题考查了等边三角形的性质，以及圆的面积的计算，正确理解：$\widehat{AD}$与弦AD围成的弓形的面积等于 $\widehat{CF}$与弦CF围成的弓形的面积相等是关键．