题目内容
5. 如图,圆O中,两条弦AB与CD相等,弧AB和弧CD的中点分别为M、N,MN与AB、CD分别相交于E、F,求证:ME=NF.
如图,圆O中,两条弦AB与CD相等,弧AB和弧CD的中点分别为M、N,MN与AB、CD分别相交于E、F,求证:ME=NF.
分析 连接MD,BN,根据圆心角、弧、弦的关系可得出$\widehat{AB}$=$\widehat{CD}$,由ASA定理得出△MDE≌△NBF,由此可得出结论.
解答 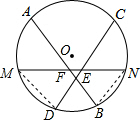 解:连接MD,BN,
解:连接MD,BN,
∴AB=CD,
∴$\widehat{AB}$=$\widehat{CD}$,
∴MD=BN.
∵$\widehat{AB}$与$\widehat{CD}$的中点分别为M、N,
∴$\widehat{DN}$=$\widehat{BM}$,$\widehat{MC}$=$\widehat{AN}$
∴∠DME=∠BNF,∠MDE=∠NBF.
在△MDE与△NBF中,
$\left\{\begin{array}{l}∠DME=∠BNF\\ MD=BN\\∠MDE=∠NBF\end{array}\right.$,
∴△MDE≌△NBF(ASA),
∴ME=NF.
点评 本题考查的是圆心角、弧、弦的关系,根据题意作出辅助线,构造出全等三角形是解答此题的关键.

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
 如图,在Rt△ABC中,∠ACB=90°,点E是AC边上的动点(点E与C、A不重合),设点M为线段BE的中点,过点E作EF⊥AB于F,连接MC、MF.
如图,在Rt△ABC中,∠ACB=90°,点E是AC边上的动点(点E与C、A不重合),设点M为线段BE的中点,过点E作EF⊥AB于F,连接MC、MF. 如图,已知△ABC内接于⊙O,AD、AE分别平分∠BAC和△BAC的外角∠BAF,且分别交圆于点D、F,连接DE,CD,DE与BC相交于点G.
如图,已知△ABC内接于⊙O,AD、AE分别平分∠BAC和△BAC的外角∠BAF,且分别交圆于点D、F,连接DE,CD,DE与BC相交于点G. 如图所示,一根长2a的木棍(AB),斜靠在与地面(OM)垂直的墙(ON)上,设木棍的中点为P,若木棍A端沿墙下滑,且B端沿地面向右滑行.请判断木棍滑动的过程中,点P到点O的距离不发生变化(用“发生”或“不发生”填空).
如图所示,一根长2a的木棍(AB),斜靠在与地面(OM)垂直的墙(ON)上,设木棍的中点为P,若木棍A端沿墙下滑,且B端沿地面向右滑行.请判断木棍滑动的过程中,点P到点O的距离不发生变化(用“发生”或“不发生”填空). 如图,已知:AD∥EF,$\frac{CF}{DF}$=$\frac{CD}{BD}$,求证:AB∥DE.
如图,已知:AD∥EF,$\frac{CF}{DF}$=$\frac{CD}{BD}$,求证:AB∥DE.