题目内容
15. 如图,在Rt△ABC中,∠ACB=90°,点E是AC边上的动点(点E与C、A不重合),设点M为线段BE的中点,过点E作EF⊥AB于F,连接MC、MF.
如图,在Rt△ABC中,∠ACB=90°,点E是AC边上的动点(点E与C、A不重合),设点M为线段BE的中点,过点E作EF⊥AB于F,连接MC、MF.(1)点B、C、E、F是否在以点M为圆心的同一个圆上?为什么?
(2)若∠CBA=56°,请问在点E运动过程中∠CMF的大小是否变化?若不变,求出∠CMF的度数;若变化,请说明理由.
分析 (1)根据直角三角形斜边上的中线等于斜边的一半得到MC=MB=ME,MF=MB=ME,得到MB=MC=ME=MF,证明结论;
(2)根据圆周角定理解答即可.
解答 解:(1)∵∠ACB=90°,点M为线段BE的中点,
∴MC=BF,即MC=MB=ME,
∵EF⊥AB,点M为线段BE的中点,
∴MF=BF,即MF=MB=ME,
∴MB=MC=ME=MF,
∴点B、C、E、F是否在以点M为圆心的同一个圆上;
(2)∵点B、C、E、F是否在以点M为圆心的同一个圆上,
∴∠CMF=2∠CBA=112°,
点E运动过程中∠CMF的大小不变.
点评 本题考查的是直角三角形的性质,掌握直角三角形斜边上的中线等于斜边的一半是解题的关键.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
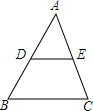 如图,△ABC中,DE∥BC,AD=6,AC=8,BD=AE,求BD的长.
如图,△ABC中,DE∥BC,AD=6,AC=8,BD=AE,求BD的长. 如图,装卸工人要把放在地面上的油桶(横截面为⊙0,半径为30cm)搬运到一辆汽车上,装卸工人先在车厢顶端C处与地平面1之间用木板搭起一个坡角为60°的斜坡BC,斜坡底端为点B,工人把油桶滚到地面A处,使它紧靠在斜坡BC的Q点上,然后用力把油桶沿斜坡推上汽车,最后使油桶停放在车厢的水平面的D处⊙01的位置,此时油桶紧靠在车厢的后挡板EF上,已知汽车车厢长CE=3.3m,车厢顶端C距离地平而1.5m,求油桶从A处滚动到D处圆心所滚过的路程(结果精确列0.1m).参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1,73,π≈3.14.
如图,装卸工人要把放在地面上的油桶(横截面为⊙0,半径为30cm)搬运到一辆汽车上,装卸工人先在车厢顶端C处与地平面1之间用木板搭起一个坡角为60°的斜坡BC,斜坡底端为点B,工人把油桶滚到地面A处,使它紧靠在斜坡BC的Q点上,然后用力把油桶沿斜坡推上汽车,最后使油桶停放在车厢的水平面的D处⊙01的位置,此时油桶紧靠在车厢的后挡板EF上,已知汽车车厢长CE=3.3m,车厢顶端C距离地平而1.5m,求油桶从A处滚动到D处圆心所滚过的路程(结果精确列0.1m).参考数据:$\sqrt{2}$≈1.41,$\sqrt{3}$≈1,73,π≈3.14. 如图,点O是两个同心圆的圆心,大圆半径OA,OB交小圆于点C,D.下列结论中正确的个数有( )
如图,点O是两个同心圆的圆心,大圆半径OA,OB交小圆于点C,D.下列结论中正确的个数有( )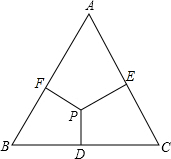 如图,P为正三角形ABC内任一点,PD⊥BC,PE⊥CA,PF⊥AB,则$\frac{PD+PE+PF}{BD+CE+AF}$=$\frac{\sqrt{3}}{3}$.
如图,P为正三角形ABC内任一点,PD⊥BC,PE⊥CA,PF⊥AB,则$\frac{PD+PE+PF}{BD+CE+AF}$=$\frac{\sqrt{3}}{3}$. 如图,圆O中,两条弦AB与CD相等,弧AB和弧CD的中点分别为M、N,MN与AB、CD分别相交于E、F,求证:ME=NF.
如图,圆O中,两条弦AB与CD相等,弧AB和弧CD的中点分别为M、N,MN与AB、CD分别相交于E、F,求证:ME=NF.