题目内容
16. 如图,已知△ABC内接于⊙O,AD、AE分别平分∠BAC和△BAC的外角∠BAF,且分别交圆于点D、F,连接DE,CD,DE与BC相交于点G.
如图,已知△ABC内接于⊙O,AD、AE分别平分∠BAC和△BAC的外角∠BAF,且分别交圆于点D、F,连接DE,CD,DE与BC相交于点G.(1)求证:DE是△ABC的外接圆的直径;
(2)设OG=3,CD=2$\sqrt{5}$,求⊙O的半径.
分析 (1)由角平分线的定义和平角关系得出∠2+∠3=90°,即∠DAE=90°,由90°的圆周角所对的弦是直径,即可得出结论;
(2)连接OC,设⊙O的半径为r,则OD=OC=r,DG=r-3,由垂径定理得出OD⊥BC,由勾股定理得出CD2-DG2=OC2-OG2,得出方程,解方程即可.
解答 (1)证明:∵AD、AE分别平分∠BAC和△BAC的外角∠BAF,
∴∠1=∠2,∠3=∠EAF,
∵∠1+∠2+∠3+∠EAF=180°,
∴∠2+∠3=90°,
即∠DAE=90°,
∴DE是△ABC的外接圆的直径;
(2)解:连接OC,如图所示:
设⊙O的半径为r,
则OD=OC=r,DG=r-3,
∵∠1=∠2,
∴$\widehat{CD}=\widehat{BD}$,
∴OD⊥BC,
∴∠OGC=∠DGC=90°,
由勾股定理得:CG2=CD2-DG2,CG2=OC2-OG2,
∴CD2-DG2=OC2-OG2,
即(2$\sqrt{5}$)2-(r-3)2=r2-32,
解得:r=5,或r=-2(不合题意,舍去),
∴⊙O的半径为5.
点评 本题考查了圆周角定理、垂径定理、勾股定理、角平分线的定义等知识;本题综合性强,有一定难度.

练习册系列答案
相关题目
8.若三条线段a、b、c满足a2+c2=b2,这三条线段组成的三角形是( )
| A. | 锐角三角形 | B. | 直角三角形 | C. | 对角三角形 | D. | 无法判断 |
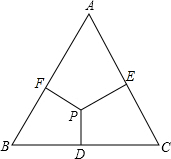 如图,P为正三角形ABC内任一点,PD⊥BC,PE⊥CA,PF⊥AB,则$\frac{PD+PE+PF}{BD+CE+AF}$=$\frac{\sqrt{3}}{3}$.
如图,P为正三角形ABC内任一点,PD⊥BC,PE⊥CA,PF⊥AB,则$\frac{PD+PE+PF}{BD+CE+AF}$=$\frac{\sqrt{3}}{3}$. 如图,圆O中,两条弦AB与CD相等,弧AB和弧CD的中点分别为M、N,MN与AB、CD分别相交于E、F,求证:ME=NF.
如图,圆O中,两条弦AB与CD相等,弧AB和弧CD的中点分别为M、N,MN与AB、CD分别相交于E、F,求证:ME=NF.