题目内容
12.当x=$\frac{-b+\sqrt{{b}^{2}-4ac}}{2a}$(a≠0,b2-4ac>0)时,代数式ax2+bx+c的值是( )| A. | 0 | B. | $\frac{-b-\sqrt{{b}^{2}-4ac}}{2a}$ | C. | -$\frac{b}{a}$ | D. | $\frac{c}{a}$ |
分析 因为一元二次方程ax2+bx+c=0(a≠0,b2-4ac>0)的根为x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$,所以代入任何一个根,方程都成立,由此得出答案即可.
解答 解:∵一元二次方程ax2+bx+c=0(a≠0,b2-4ac>0)的根为x=$\frac{-b±\sqrt{{b}^{2}-4ac}}{2a}$,
∴当x=$\frac{-b+\sqrt{{b}^{2}-4ac}}{2a}$时,ax2+bx+c=0.
故选:A.
点评 此题考查解一元二次方程的方法-公式法,一元二次方程的解,关键是掌握求根公式.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
4.a为任意实数,一次函数y=ax-2a+1的图象必过一定点,此顶点的坐标为( )
| A. | (0,1) | B. | (1,2) | C. | (2,1) | D. | (2,0) |
9.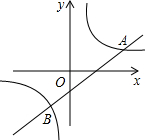 如图所示,一次函数y=kx+b和反比例函数y=$\frac{a}{x}$都经过A(2,1),B(-1,-2)两点,则不等式kx+b>$\frac{a}{x}$的解集为( )
如图所示,一次函数y=kx+b和反比例函数y=$\frac{a}{x}$都经过A(2,1),B(-1,-2)两点,则不等式kx+b>$\frac{a}{x}$的解集为( )
 如图所示,一次函数y=kx+b和反比例函数y=$\frac{a}{x}$都经过A(2,1),B(-1,-2)两点,则不等式kx+b>$\frac{a}{x}$的解集为( )
如图所示,一次函数y=kx+b和反比例函数y=$\frac{a}{x}$都经过A(2,1),B(-1,-2)两点,则不等式kx+b>$\frac{a}{x}$的解集为( )| A. | x>2 | B. | x>-1 | C. | -1<x<0或x>2 | D. | x<-1或0<x<2 |
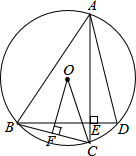 如图.点A、B、C、D在⊙O上,AC⊥BD于点E,过点O作OF⊥BC于F,
如图.点A、B、C、D在⊙O上,AC⊥BD于点E,过点O作OF⊥BC于F, 如图:抛物线y1=$\frac{1}{2}$x2+(m-5)x+2m与直线y2=2x-4交于x轴上A点和另一点B.
如图:抛物线y1=$\frac{1}{2}$x2+(m-5)x+2m与直线y2=2x-4交于x轴上A点和另一点B. 如图,在Rt△ABC中,∠ACB=90°,AB=4.分别以AC,BC为直径作半圆,面积分别记为S1,S2,则S1+S2的值等于( )
如图,在Rt△ABC中,∠ACB=90°,AB=4.分别以AC,BC为直径作半圆,面积分别记为S1,S2,则S1+S2的值等于( )