题目内容
3. 如图:抛物线y1=$\frac{1}{2}$x2+(m-5)x+2m与直线y2=2x-4交于x轴上A点和另一点B.
如图:抛物线y1=$\frac{1}{2}$x2+(m-5)x+2m与直线y2=2x-4交于x轴上A点和另一点B.(1)求A、B两点的坐标;
(2)观察图象回答:当x取何值时,①y1=y2;②y1>y2;③y1<y2;
(3)若y1、y2都随x的增加而增加,求x的取值范围.
分析 (1)先求出A点坐标,再代入抛物线y1=$\frac{1}{2}$x2+(m-5)x+2m求出m的值即可得出其解析式,联立两直线的解析式即可得出B点坐标;
(2)根据两函数图象的交点即可得出结论;
(3)求出抛物线的对称轴方程,根据一次函数与二次函数的性质即可得出结论.
解答 解:(1)∵点A在直线y2=2x-4上,
∴2x-4=0,解得x=2,
∴A(2,0).
∵点A在抛物线y1=$\frac{1}{2}$x2+(m-5)x+2m上,
∴2+2(m-5)+2m=0,解得m=2,
∴抛物线的解析式为y1=$\frac{1}{2}$x2-3x+4,
∴$\left\{\begin{array}{l}{y}_{1}=\frac{1}{2}{x}^{2}-3x+4\\{y}_{2}=2x-4\end{array}\right.$,解得$\left\{\begin{array}{l}x=2\\ y=0\end{array}\right.$或$\left\{\begin{array}{l}x=8\\ y=12\end{array}\right.$,
∴B(8,12);
(2)①由函数图象可知,当x=2或x=8时,y1=y2;
②由函数图象可知,当2<x<8时,y1>y2;
③由函数图象可知,当x<2或x>8时,y1<y2;
(3)∵抛物线的解析式为y1=$\frac{1}{2}$x2-3x+4,
∴其对称轴为x=-$\frac{-3}{2×\frac{1}{2}}$=3,
∴当x>3时,y1、y2都随x的增加而增加.
点评 本题考查的是二次函数与不等式.能根据题意利用数形结合求出不等式的解集是解答此题的关键.

练习册系列答案
相关题目
8.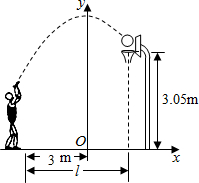 如图,小姚身高$\frac{9}{4}$m在某次投篮中,球的运动路线是抛物线y=-$\frac{1}{5}$x2+$\frac{7}{2}$的一部分,若命中篮圈中心,则他与篮底的距离是( )
如图,小姚身高$\frac{9}{4}$m在某次投篮中,球的运动路线是抛物线y=-$\frac{1}{5}$x2+$\frac{7}{2}$的一部分,若命中篮圈中心,则他与篮底的距离是( )
 如图,小姚身高$\frac{9}{4}$m在某次投篮中,球的运动路线是抛物线y=-$\frac{1}{5}$x2+$\frac{7}{2}$的一部分,若命中篮圈中心,则他与篮底的距离是( )
如图,小姚身高$\frac{9}{4}$m在某次投篮中,球的运动路线是抛物线y=-$\frac{1}{5}$x2+$\frac{7}{2}$的一部分,若命中篮圈中心,则他与篮底的距离是( )| A. | 3.5m | B. | 4m | C. | 4.5m | D. | 4.6m |
12.当x=$\frac{-b+\sqrt{{b}^{2}-4ac}}{2a}$(a≠0,b2-4ac>0)时,代数式ax2+bx+c的值是( )
| A. | 0 | B. | $\frac{-b-\sqrt{{b}^{2}-4ac}}{2a}$ | C. | -$\frac{b}{a}$ | D. | $\frac{c}{a}$ |
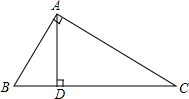 如图,在Rt△ABC中,∠BAC=90°,AD⊥BC,BD:CD=1:4.
如图,在Rt△ABC中,∠BAC=90°,AD⊥BC,BD:CD=1:4.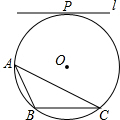 如图,⊙O是△ABC的外接圆,半径为4,直线l与⊙O相切,切点为P,l∥BC,l与BC间的距离为7.
如图,⊙O是△ABC的外接圆,半径为4,直线l与⊙O相切,切点为P,l∥BC,l与BC间的距离为7.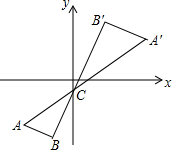 如图,将△ABC以点C(0,-1)为位似中心放大2倍,得到△A′B′C′,点A′的坐标为(a,b),则点A的坐标为(-$\frac{1}{2}$a,-$\frac{1}{2}$b-$\frac{3}{2}$).
如图,将△ABC以点C(0,-1)为位似中心放大2倍,得到△A′B′C′,点A′的坐标为(a,b),则点A的坐标为(-$\frac{1}{2}$a,-$\frac{1}{2}$b-$\frac{3}{2}$).