题目内容
4．a为任意实数，一次函数y=ax-2a+1的图象必过一定点，此顶点的坐标为（ ）| A． | （0，1） | B． | （1，2） | C． | （2，1） | D． | （2，0） |
分析 由于x=2时，函数值恒为1，于是根据一次函数图象上点的坐标特征即可对各选项进行判断．
解答 解：∵y=ax-2a+1，
∴当x=2时，y=2a-2a+1=1，
∴一次函数y=ax-2a+1的图象必过点（2，1）．
故选C．
点评 本题考查了一次函数图象上点的坐标特征：直线上任意一点的坐标都满足函数关系式y=kx+b．
练习册系列答案
字词句篇与同步作文达标系列答案
相关题目
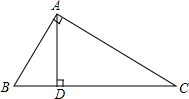如图，在Rt△ABC中，∠BAC=90°，AD⊥BC，BD：CD=1：4．
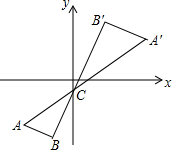如图，将△ABC以点C（0，-1）为位似中心放大2倍，得到△A′B′C′，点A′的坐标为（a，b），则点A的坐标为（-$\frac{1}{2}$a，-$\frac{1}{2}$b-$\frac{3}{2}$）．
12．当x=$\frac{-b+\sqrt{{b}^{2}-4ac}}{2a}$（a≠0，b2-4ac＞0）时，代数式ax2+bx+c的值是（ ）
| A． | 0 | B． | $\frac{-b-\sqrt{{b}^{2}-4ac}}{2a}$ | C． | -$\frac{b}{a}$ | D． | $\frac{c}{a}$ |
如图所示，∠1=∠2，AC=AD．可利用SAS来判定△ABC≌△ABD．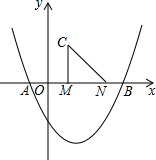
如图，二次函数y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2的图象与x轴交于点A，B，点M，N在x轴上，点N在点M右侧，MN=2，以MN为直角边向上作等腰直角三角形CMN，∠CMN=90°，设点M的横坐标为m．
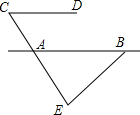如图，AB∥CD，∠C=60°，∠ABE=42°，则∠E的度数为78°．