题目内容
2.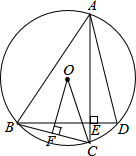 如图.点A、B、C、D在⊙O上,AC⊥BD于点E,过点O作OF⊥BC于F,
如图.点A、B、C、D在⊙O上,AC⊥BD于点E,过点O作OF⊥BC于F,(1)求证:△AEB∽△OFC;
(2)求证:AE•BC=AD•BE;
(3)若AD=8,求OF的长.
分析 (1)利用圆周角定理得出∠BAC=∠FOC,进而得出△AEB∽△OFC;
(2)根据圆周角定理得到∠CBD=∠CAD,∠AED=∠BEC,推出△ADE∽△CBE,根据相似三角形的性质即可得到结论;
(3)利用相似三角形的性质得出$\frac{OF}{FC}=\frac{AD}{BC}$,进而得出OF的长.
解答 (1)证明:连接BO, ∵AC⊥BD,OF⊥BC,
∵AC⊥BD,OF⊥BC,
∴∠AEB=90°,∠CFO=90°,
∵OF⊥BC,
∴∠COF=$\frac{1}{2}$,
∵∠BAC=$\frac{1}{2}$∠BOC,
∴∠BAC=∠FOC,
∴△AEB∽△OFC;
(2)证明:∵∠CBD=∠CAD,∠AED=∠BEC,
∴△ADE∽△CBE,
∴$\frac{AD}{BC}=\frac{AE}{BE}$,
∴AE•BC=AD•BE;
(3)解:由(1)知,△AEB∽△OFC,
∴$\frac{AE}{BE}=\frac{OF}{FC}$,
∵$\frac{AD}{BC}=\frac{AE}{BE}$,
∴$\frac{OF}{FC}=\frac{AD}{BC}$,
∴$\frac{OF}{AD}=\frac{CF}{BC}$=$\frac{1}{2}$,
∴OF=$\frac{1}{2}$AD=4.
点评 此题主要考查了相似三角形的判定与性质和圆周角定理等知识,熟练利用圆周角定理得出相等的角是解题关键.

练习册系列答案
相关题目
10.$\sqrt{{x^2}-4x+4}$=x-2,则( )
| A. | x>-2 | B. | x≥2 | C. | x<-2 | D. | x≥-2 |
12.当x=$\frac{-b+\sqrt{{b}^{2}-4ac}}{2a}$(a≠0,b2-4ac>0)时,代数式ax2+bx+c的值是( )
| A. | 0 | B. | $\frac{-b-\sqrt{{b}^{2}-4ac}}{2a}$ | C. | -$\frac{b}{a}$ | D. | $\frac{c}{a}$ |
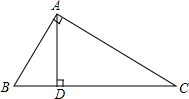 如图,在Rt△ABC中,∠BAC=90°,AD⊥BC,BD:CD=1:4.
如图,在Rt△ABC中,∠BAC=90°,AD⊥BC,BD:CD=1:4.