题目内容
10．
如图，在Rt△ABC中，∠ACB=90°，AB=4．分别以AC，BC为直径作半圆，面积分别记为S1，S2，则S1+S2的值等于（ ）| A． | 2π | B． | 3π | C． | 4π | D． | 8π |
分析 根据半圆面积公式结合勾股定理，知S1+S2等于以斜边为直径的半圆面积．
解答 解：∵S1=$\frac{1}{2}$π（$\frac{AC}{2}$）2=$\frac{1}{8}$πAC2，S2=$\frac{1}{8}$πBC2，
∴S1+S2=$\frac{1}{8}$π（AC2+BC2）=$\frac{1}{8}$πAB2=2π．
故选A．
点评 本题考查的是勾股定理，熟知在任何一个直角三角形中，两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键．
练习册系列答案
赢在课堂名师课时计划系列答案
相关题目
12．当x=$\frac{-b+\sqrt{{b}^{2}-4ac}}{2a}$（a≠0，b2-4ac＞0）时，代数式ax2+bx+c的值是（ ）
| A． | 0 | B． | $\frac{-b-\sqrt{{b}^{2}-4ac}}{2a}$ | C． | -$\frac{b}{a}$ | D． | $\frac{c}{a}$ |
5．
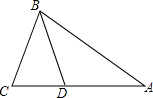如图，在△ABC中，AB=AC，∠A=36°，BD平分∠ABC交AC于点D，若AC=2a，则AD的长是（ ）
如图，在△ABC中，AB=AC，∠A=36°，BD平分∠ABC交AC于点D，若AC=2a，则AD的长是（ ）| A． | $\frac{\sqrt{5}-1}{2}$a | B． | $\frac{\sqrt{5}+1}{2}$a | C． | （$\sqrt{5}$-1）a | D． | （$\sqrt{5}$+1）a |
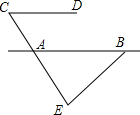如图，AB∥CD，∠C=60°，∠ABE=42°，则∠E的度数为78°．
一个无盖长方体盒子的容积是V．