题目内容
7.计算:(1)3+6+9+12+…+2019;
(2)a+(a+b)+(a+2b)+(a+3b)+…(a+99b)
分析 (1)根据等差数列求和公式即可求解;
(2)先变形为100a+(b+2b+3b+…+99b),再根据等差数列求和公式即可求解.
解答 解:(1)3+6+9+12+…+2019
=(3+2019)×673÷2
=2022×673÷2
=680403;
(2)a+(a+b)+(a+2b)+(a+3b)+…(a+99b)
=100a+(b+2b+3b+…+99b)
=100a+$\frac{1}{2}$(1+99)×99b
=100a+4950b.
点评 考查了整式的加减,有理数的加法,关键是灵活运用运算定律简便计算.

练习册系列答案
 黄冈创优卷系列答案
黄冈创优卷系列答案
相关题目
2.点C是线段AB上一点,D是线段BC的中点.若AD=5cm.则AC+AB等于( )
| A. | 8cm | B. | 10cm | C. | 12cm | D. | 不确定 |
12.当x=$\frac{-b+\sqrt{{b}^{2}-4ac}}{2a}$(a≠0,b2-4ac>0)时,代数式ax2+bx+c的值是( )
| A. | 0 | B. | $\frac{-b-\sqrt{{b}^{2}-4ac}}{2a}$ | C. | -$\frac{b}{a}$ | D. | $\frac{c}{a}$ |
5.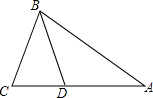 如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,若AC=2a,则AD的长是( )
如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,若AC=2a,则AD的长是( )
 如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,若AC=2a,则AD的长是( )
如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,若AC=2a,则AD的长是( )| A. | $\frac{\sqrt{5}-1}{2}$a | B. | $\frac{\sqrt{5}+1}{2}$a | C. | ($\sqrt{5}$-1)a | D. | ($\sqrt{5}$+1)a |
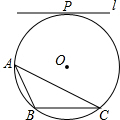 如图,⊙O是△ABC的外接圆,半径为4,直线l与⊙O相切,切点为P,l∥BC,l与BC间的距离为7.
如图,⊙O是△ABC的外接圆,半径为4,直线l与⊙O相切,切点为P,l∥BC,l与BC间的距离为7.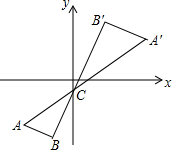 如图,将△ABC以点C(0,-1)为位似中心放大2倍,得到△A′B′C′,点A′的坐标为(a,b),则点A的坐标为(-$\frac{1}{2}$a,-$\frac{1}{2}$b-$\frac{3}{2}$).
如图,将△ABC以点C(0,-1)为位似中心放大2倍,得到△A′B′C′,点A′的坐标为(a,b),则点A的坐标为(-$\frac{1}{2}$a,-$\frac{1}{2}$b-$\frac{3}{2}$). 如图所示,∠1=∠2,AC=AD.可利用SAS来判定△ABC≌△ABD.
如图所示,∠1=∠2,AC=AD.可利用SAS来判定△ABC≌△ABD.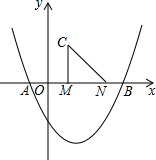 如图,二次函数y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2的图象与x轴交于点A,B,点M,N在x轴上,点N在点M右侧,MN=2,以MN为直角边向上作等腰直角三角形CMN,∠CMN=90°,设点M的横坐标为m.
如图,二次函数y=$\frac{1}{2}$x2-$\frac{3}{2}$x-2的图象与x轴交于点A,B,点M,N在x轴上,点N在点M右侧,MN=2,以MN为直角边向上作等腰直角三角形CMN,∠CMN=90°,设点M的横坐标为m.