题目内容
19.如图1,以矩形OABC的顶点O为原点,OA所在的直线为x轴,OC所在的直线为y轴,建立平面直角坐标系,已知OA=3,OC=2,点E是AB的中点,在OA上取一点D,将△BDA沿BD翻折,使点A落在BC边上的点F处.(Ⅰ)直接写出点E、F的坐标;
(Ⅱ)如图2,若点P是线段DA上的一个动点,过P作PH⊥DB于H点,设OP的长为x,△DPH的面积为S,试用关于x的代数式表示S;
(Ⅲ)如图3,在x轴、y轴上是否分别存在点M、N,使得四边形MNFE的周长最小?如果存在,求出周长的最小值.(直接写出结果即可)
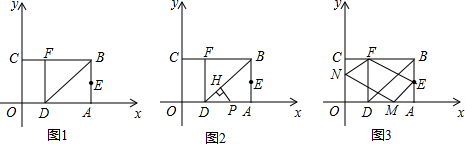
分析 (Ⅰ)求出CF和AE的长度即可写出点的坐标;
(Ⅱ)用x表示出PD长度,结合三角函数进一步表示DH,PH的长度,运用三角形面积公式即可求解;
(Ⅲ)作点F关于y轴的对称点F′,点E关于x轴的对称点E′,连接E′F′交y轴于点N,交x轴于点M,此时四边形MNFE的周长最小,求出E′和F′的坐标直接求线段长度即可.
解答 解:(Ⅰ)由题意可求,AE=1,CF=1,
故:E(3,1),F(1,2);
(Ⅱ)如图2
∵将△BDA沿BD翻折,使点A落在BC边上的点F处,
∴BF=AB=2,
∴OD=CF=3-2=1,
若设OP的长为x,
则,PD=x-1,
在Rt△ABD中,AB=2,AD=2,
∴∠ADB=45°,
在Rt△PDH中,PH=DH=DP×$\frac{\sqrt{2}}{2}$=$\frac{\sqrt{2}}{2}$(x-1),
∴S=$\frac{1}{2}$×DH×PH=$\frac{1}{2}$×$\frac{\sqrt{2}}{2}$(x-1)×$\frac{\sqrt{2}}{2}$(x-1)=$\frac{{x}^{2}}{4}$-$\frac{x}{2}$+$\frac{1}{4}$;
(Ⅲ)如图3
作点F关于y轴的对称点F′,点E关于x轴的对称点E′,连接E′F′交y轴于点N,交x轴于点M,此时四边形MNFE的周长最小,
可求,点F(1,2)关于y轴的对称点F′(-1,2),点E(3,1)关于x轴的对称点E′(3,-1),
用两点法可求直线E′F′的解析式为:y=$-\frac{3}{4}x+\frac{5}{4}$,
当x=0时,y=$\frac{5}{4}$,当y=0时,x=$\frac{5}{3}$,
∴N(0,$\frac{5}{4}$),M($\frac{5}{3}$,0),
此时,四边形MNFE的周长=E′F′+EF=$\sqrt{(-1-3)^{2}+(2+1)^{2}}$+$\sqrt{{2}^{2}+{1}^{2}}$=5+$\sqrt{5}$;
∴在x轴、y轴上分别存在点M、N,使得四边形MNFE的周长最小,最小为:5+$\sqrt{5}$.
点评 此题主要考查几何变换中的翻折,熟悉翻折的性质,会结合坐标系求点的坐标,会运用对称点解决线段和最小是解题的关键.

 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案| A. | x+5>0 | B. | x+5<0 | C. | -(x+5)2<0 | D. | (x+5)2≥0 |
| A. | a-3>b-3 | B. | -3a>-3b | C. | $\frac{a}{3}$>$\frac{b}{3}$ | D. | a+3>b+3 |
| A. | -3 | B. | 3 | C. | 0 | D. | 2 |
| A. | 在1到2之间 | B. | 在2到3之间 | C. | 在3到4之间 | D. | 在4到5之间 |