题目内容
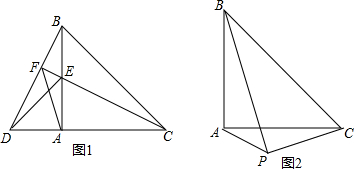
11.在三角形ABC中,∠BAC=90°,AB=AC.(1)如图1,点D是CA延长线上一点,点E在线段AB上,且AD=AE,连接BD和CE,延长CE交BD于点F,连接AF.求证:BD=CE;
(2)在(1)得条件下,求∠AFD的度数;
(3)如图2,点P是△ABC外一点,∠APB=45°,猜想PA、PB、PC三条线段长度之间存在的等量关系,并证明你的结论.
分析 (1)由两个等腰直角三角形得到两个三角形全等的条件,即可;
(2)利用(1)得到的结论,判断出点A,E,F,D四点共圆,即可;
(3)利用三角形相似的判定和性质,再利用勾股定理,即可.
解答 证明:(1)∵∠BAC=90°,
∴∠BAC=∠DAB=90°,
在Rt△EAC和Rt△DAB中,
$\left\{\begin{array}{l}{AD=AE}\\{∠DAB=EAC}\\{AB=AC}\end{array}\right.$,
∴Rt△EAC≌Rt△DAB,
∴CE=BD;
(2)如图1,
由(1)有,Rt△EAC≌Rt△DAB,
∴∠ABD=∠ACE,
∵∠ACE+∠AEC=90°,
∴∠ABD+∠AEC=∠ABD+∠BEF=90°,
∵∠DAE=90°,
∴点A,E,F,D四点共圆,
∴∠AFE=∠ADE=45°,
∴∠AFD=45°;
(3)PA、PB、PC三条线段长度之间存在的等量关系为PB-PC=$\sqrt{2}$PA.
如图2,在PB上截取PM=PC,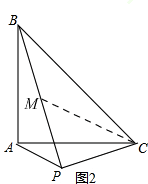
由(2)有,∠BPC=90°,
∴CM=$\sqrt{2}$PC,∠PMC=45°,
∴∠BMC=135°,
∵∠APB=45°,
∴∠APC=135°,
∴∠APC=∠BMC,
∵∠ACP+∠ACM=∠BCM+∠ACM=45°,
∴∠ACP=∠BCM,
∴△APC∽△BMC,
∴$\frac{PC}{CM}=\frac{PA}{MB}$=$\frac{1}{\sqrt{2}}$,
∴BM=$\sqrt{2}$PA,
∴PB=PM+BM=PC+$\sqrt{2}$PA,
∴PB-PC=$\sqrt{2}$PA.
点评 此题是三角形综合题,主要考查了全等三角形,相似三角形的性质和判定,判定四点共圆的方法和同弧所对圆周角相等,判断四点共圆是解本题的关键,也是难点.

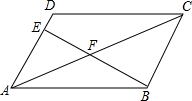 如图,在平行四边形ABCD中,AE:AD=2:3,连接BE交AC于点F,若△ABF和四边形CDEF的面积分别记为S1,S2,则S1:S2为( )
如图,在平行四边形ABCD中,AE:AD=2:3,连接BE交AC于点F,若△ABF和四边形CDEF的面积分别记为S1,S2,则S1:S2为( )| A. | 2:3 | B. | 4:9 | C. | 6:11 | D. | 6:13 |