题目内容
11．计算下列各题：（1）（-1）-（-7）+（-8）
（2）-$\frac{1}{3}$÷（-3）×（-$\frac{1}{3}$）
（3）（$\frac{1}{5}$-$\frac{1}{2}$-$\frac{5}{12}$）+（-$\frac{1}{60}$）
（4）-125+（-25）-64+（-4）
（5）（-2）4÷（-8）-（-$\frac{1}{2}$）3×（-22）
分析 （1）（2）（4）从左向右依次计算，求出算式的值是多少即可．
（3）首先计算小括号里面的算式，然后计算小括号外面的算式即可．
（5）首先计算除法和乘法，然后计算减法，求出算式的值是多少即可．
解答 解：（1）（-1）-（-7）+（-8）
=6-8
=-2
（2）-$\frac{1}{3}$÷（-3）×（-$\frac{1}{3}$）
=$\frac{1}{9}$×（-$\frac{1}{3}$）
=-$\frac{1}{27}$
（3）（$\frac{1}{5}$-$\frac{1}{2}$-$\frac{5}{12}$）+（-$\frac{1}{60}$）
=（-$\frac{43}{60}$）+（-$\frac{1}{60}$）
=-$\frac{11}{15}$
（4）-125+（-25）-64+（-4）
=-150-64-4
=-218
（5）（-2）4÷（-8）-（-$\frac{1}{2}$）3×（-22）
=16÷（-8）-（-$\frac{1}{8}$）×4
=-2+0.5
=-1.5
点评 此题主要考查了有理数的混合运算，要熟练掌握，注意明确有理数混合运算顺序：先算乘方，再算乘除，最后算加减；同级运算，应按从左到右的顺序进行计算；如果有括号，要先做括号内的运算．
练习册系列答案
相关题目
如图，在平面直角坐标系内，梯形OABC的顶点坐标分别是：A（3，4），B（8，4），C（11，0），点P（t，0）是线段OC上一点，设四边形ABCP的面积为S．
19．
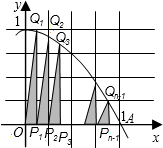如图，记抛物线y=-x2+1的图象与x正半轴的交点为A，将线段OA分成n等份，设分点分别为P1，P2，…，Pn-1，过每个分点作x轴的垂线，分别与抛物线交于点Q1，Q2，…，Qn-1，再记直角三角形OP1Q1，P1P2Q2，…的面积分别为S1，S2，…，这样就有S1=$\frac{{{n^2}-1}}{{2{n^3}}}，{S_2}=\frac{{{n^2}-4}}{{2{n^3}}}$，…；记W=S1+S2+…+Sn-1，当n越来越大时，你猜想W最接近的常数是（ ）
如图，记抛物线y=-x2+1的图象与x正半轴的交点为A，将线段OA分成n等份，设分点分别为P1，P2，…，Pn-1，过每个分点作x轴的垂线，分别与抛物线交于点Q1，Q2，…，Qn-1，再记直角三角形OP1Q1，P1P2Q2，…的面积分别为S1，S2，…，这样就有S1=$\frac{{{n^2}-1}}{{2{n^3}}}，{S_2}=\frac{{{n^2}-4}}{{2{n^3}}}$，…；记W=S1+S2+…+Sn-1，当n越来越大时，你猜想W最接近的常数是（ ）| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{4}$ | D． | $\frac{2}{3}$ |
如图，是一所小区前的一块长方形空地，在空地中规划建设一个长方形和半圆的建筑物，其余部分进行绿化，用式子表示这块空地的绿化面积．
如图，在Rt△AOB中，OA=OB=3$\sqrt{2}$，⊙O的半径为$\sqrt{2}$，点P是AB边上的一动点，过点P作⊙O的一条切线PQ（点Q为切点），则PQ长度的取值范围为$\sqrt{7}$≤PQ≤4．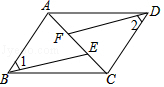
如图，已知点A、F、E、C在同一直线上，AB∥CD，∠1=∠2，AF=CE．