题目内容
16. 如图,在Rt△AOB中,OA=OB=3$\sqrt{2}$,⊙O的半径为$\sqrt{2}$,点P是AB边上的一动点,过点P作⊙O的一条切线PQ(点Q为切点),则PQ长度的取值范围为$\sqrt{7}$≤PQ≤4.
如图,在Rt△AOB中,OA=OB=3$\sqrt{2}$,⊙O的半径为$\sqrt{2}$,点P是AB边上的一动点,过点P作⊙O的一条切线PQ(点Q为切点),则PQ长度的取值范围为$\sqrt{7}$≤PQ≤4.
分析 首先连接OP、OQ,根据勾股定理知PQ2=OP2-OQ2,可得当OP⊥AB时,即线段PQ最短,然后由勾股定理即可求得答案.
解答 解:连接OP、OQ.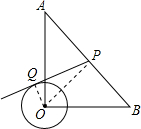
∵PQ是⊙O的切线,
∴OQ⊥PQ;
根据勾股定理知PQ2=OP2-OQ2,
∴当PO⊥AB时,线段PQ最短,
∵在Rt△AOB中,OA=OB=3$\sqrt{2}$,
∴AB=$\sqrt{2}$OA=6,
∴OP=$\frac{OA•OB}{AB}$=3,
∴PQ=$\sqrt{O{P}^{2}-O{Q}^{2}}$=$\sqrt{7}$,
当点P与点B或点A重合时,PQ=$\sqrt{O{B}^{2}-O{Q}^{2}}$=4,
∴$\sqrt{7}$≤PQ≤4.
故答案为:$\sqrt{7}$≤PQ≤4.
点评 本题考查了切线的性质、等腰直角三角形的性质以及勾股定理.此题难度适中,注意掌握辅助线的作法,注意得到当PO⊥AB时,线段PQ最短是关键.

练习册系列答案
相关题目
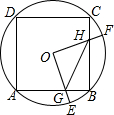 如图,边长为4的正方形ABCD内接于⊙O,点E是AB上的一动点(不与A,B重合),点F是BC上的一点,连接OE,OF,分别与AB,BC交于点G,H,且∠EOF=90°.
如图,边长为4的正方形ABCD内接于⊙O,点E是AB上的一动点(不与A,B重合),点F是BC上的一点,连接OE,OF,分别与AB,BC交于点G,H,且∠EOF=90°.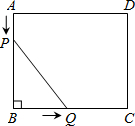 在矩形ABCD中,已知AB=5cm,BC=6cm,点P从点A开始沿边AB向终点B以1cm/s的速度运动;同时,点Q从点B开始沿边BC向终点C以2cm/s的速度运动.当点Q运动到点C时,两点停止运动.设运动时间为t秒.
在矩形ABCD中,已知AB=5cm,BC=6cm,点P从点A开始沿边AB向终点B以1cm/s的速度运动;同时,点Q从点B开始沿边BC向终点C以2cm/s的速度运动.当点Q运动到点C时,两点停止运动.设运动时间为t秒.