题目内容
2. 如图,在平面直角坐标系内,梯形OABC的顶点坐标分别是:A(3,4),B(8,4),C(11,0),点P(t,0)是线段OC上一点,设四边形ABCP的面积为S.
如图,在平面直角坐标系内,梯形OABC的顶点坐标分别是:A(3,4),B(8,4),C(11,0),点P(t,0)是线段OC上一点,设四边形ABCP的面积为S.(1)过点B作BE⊥x轴于点E,则BE=4,用含t的代数式表示PC=11-t.
(2)求S与t的函数关系.
(3)当S=20时,直接写出线段CP的长?
(4)求线段BC的长.
分析 (1)过点B作BE⊥X轴于点E,根据B(8,4),即可求得BE=4,由于C(11,0),点P(t,0),于是得到OC=11,OP=t,即可得到结论;
(2)根据梯形面积公式S=$\frac{1}{2}$(AB+PC)BE,代入数据即可得到结论;
(3)由S=20,解得t=6,把t=6代入PC=11-t,即可得到结论;
(4)首先过点A作AF⊥x轴于点F,进而得出△OFA≌△CEB(SAS),即可得出答案.
解答 解:(1)过点B作BE⊥x轴于点E,
∵B(8,4),
∴BE=4,
∵C(11,0),点P(t,0),
∴OC=11,OP=t,
∴用含t的代数式表示PC=11-t;
故答案为:4,11-t;
(2)根据梯形的面积公式得:S=$\frac{1}{2}$(AB+PC)BE,=$\frac{1}{2}$(5+11-t)×4,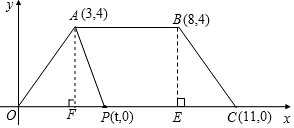
∴S与t的函数关系为:S=-2t+32,
(3)把S=20代入S=-2t+32,
解得:t=6,
故CP=11-t=11-6=5;
(4)过点A作AF⊥x轴于点F,
∵A(3,4),
∴OF=3,AF=4,
∴AO=5,
∵B(8,0),C(11,0),
∴BE=4,EC=3,
在△OFA和△CEB中,
∵$\left\{\begin{array}{l}{OF=EC}\\{∠OFA=∠CEB}\\{AF=BE}\end{array}\right.$,
∴△OFA≌△CEB(SAS),
∴OA=BC=5.
点评 此题主要考查了全等三角形的判定与性质以及勾股定理、梯形面积求法等知识,正确表示出PC的长是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
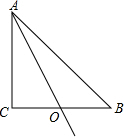 如图,在△ABC中,∠ACB=90°,AC=BC=2,O是BC的中点,P是射线AO上的一个动点,则当∠BPC=90°时,AP的长为$\sqrt{5}$-1或$\sqrt{5}$+1.
如图,在△ABC中,∠ACB=90°,AC=BC=2,O是BC的中点,P是射线AO上的一个动点,则当∠BPC=90°时,AP的长为$\sqrt{5}$-1或$\sqrt{5}$+1.