题目内容
【材料阅读】如图(1),已知点A、B是直线l同侧的两点,点P在直线l上,问点P在何处时,才能使PA+PB最小?
作法:以直线l为对称轴作点A的对称点A′,连接A′B,交直线l于点P,则点P为满足条件的点.
证明:在直线l上任取另一点Q,连接PA、QA、QB.
∵点A与A′关于直线l成轴对称,点P、Q在直线l上
∴PA=PA′,QA=QA′.
∵QA′+QB>A′B,
∴QA+QB>A′B
即QA+QB>A′P+BP,
∴QA+QB>AP+BP.
∴PA+PB最小.
【方法应用】如图(2),Rt△ABC中,∠B=90°,AB=BC=2,点D是斜边AC的中点.点P在AB上,则点P在何处时,才能使PC+PD最小?请在图(2)中画出点P的位置(保留痕迹,不要求证明),并直接写出PC+PD的最小值.
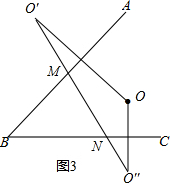
【问题解决】如图(3),已知∠ABC=45°,点O是∠ABC内一点,且OB=
.点M、N分别在AB和BC上,则点M、N分别在何处时,才能使OM+MN+NO最小?请在图(3)中画出点M、N的位置(保留痕迹,不要求证明),并直接写出OM+MN+NO的最小值.
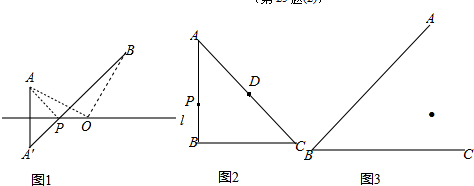
作法:以直线l为对称轴作点A的对称点A′,连接A′B,交直线l于点P,则点P为满足条件的点.
证明:在直线l上任取另一点Q,连接PA、QA、QB.
∵点A与A′关于直线l成轴对称,点P、Q在直线l上
∴PA=PA′,QA=QA′.
∵QA′+QB>A′B,
∴QA+QB>A′B
即QA+QB>A′P+BP,
∴QA+QB>AP+BP.
∴PA+PB最小.
【方法应用】如图(2),Rt△ABC中,∠B=90°,AB=BC=2,点D是斜边AC的中点.点P在AB上,则点P在何处时,才能使PC+PD最小?请在图(2)中画出点P的位置(保留痕迹,不要求证明),并直接写出PC+PD的最小值.
【问题解决】如图(3),已知∠ABC=45°,点O是∠ABC内一点,且OB=
| 2 |

考点:轴对称-最短路线问题,勾股定理
专题:阅读型
分析:【方法应用】如图(2),延长CB至C′,使C′B=CB,连结C′D交AB于P,则点P为所求.利用勾股定理即可求解;
【问题解决】如图(3),分别作点O关于BA、BC的对称点O′、O′′,连结O′O′′交BA、BC于点M、N,则点M、N为所求.在Rt△O′BO′′中利用勾股定理即可求解.
【问题解决】如图(3),分别作点O关于BA、BC的对称点O′、O′′,连结O′O′′交BA、BC于点M、N,则点M、N为所求.在Rt△O′BO′′中利用勾股定理即可求解.
解答: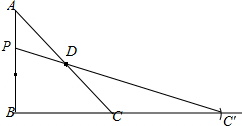 解:(1)画图正确.
解:(1)画图正确.
延长CB至C′,使C′B=CB,连结C′D交AB于P,
则点P为所求.
PC+PD的最小值为
.
PC+PD最小值即为C′D的长,过D作DE⊥BC,
E为垂足,易知DE=BE=1,在Rt△DE C′中,
C′D=
=
;
(2)画图正确.
分别作点O关于BA、BC的对称点O′、O′′,
连结O′O′′交BA、BC于点M、N,则点M、N为所求.
OM+MN+NO最小值为2.
OM+MN+NO最小值即为O′O′′的长,连结O′B、O′′B,
易知∠O′B O′′=90°,O′B=O′′B=OB=
,
在Rt△O′BO′′中,O′O′′=
=2.
 解:(1)画图正确.
解:(1)画图正确.延长CB至C′,使C′B=CB,连结C′D交AB于P,
则点P为所求.
PC+PD的最小值为
| 10 |
PC+PD最小值即为C′D的长,过D作DE⊥BC,
E为垂足,易知DE=BE=1,在Rt△DE C′中,
C′D=
| C′E2+DE2 |
| 10 |

(2)画图正确.
分别作点O关于BA、BC的对称点O′、O′′,
连结O′O′′交BA、BC于点M、N,则点M、N为所求.
OM+MN+NO最小值为2.
OM+MN+NO最小值即为O′O′′的长,连结O′B、O′′B,
易知∠O′B O′′=90°,O′B=O′′B=OB=
| 2 |
在Rt△O′BO′′中,O′O′′=
| O′B2+O″B2 |
点评:本题考查了轴对称,以及勾股定理,正确确定如何使线段的和最小是关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案
相关题目
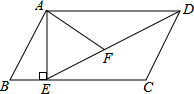 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.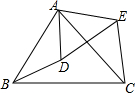 如图,D为△ABC内一点,E为△ABC外一点,且满足
如图,D为△ABC内一点,E为△ABC外一点,且满足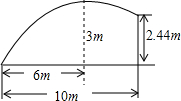 如图,在一次足球训练中,球员小王从球门前方10m起脚射门,球的运行路线恰是一条抛物线,当球飞行的水平距离是6m时,球到达最高点,此时球高约3m.已知球门高2.44m.问此球能否射进球门?
如图,在一次足球训练中,球员小王从球门前方10m起脚射门,球的运行路线恰是一条抛物线,当球飞行的水平距离是6m时,球到达最高点,此时球高约3m.已知球门高2.44m.问此球能否射进球门?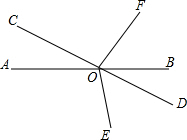 如图,直线AB、CD相交于点O,∠EOD=∠BOF,∠AOE与∠COF相等吗?为什么?
如图,直线AB、CD相交于点O,∠EOD=∠BOF,∠AOE与∠COF相等吗?为什么?