题目内容
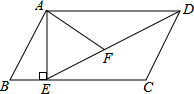 如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.(1)求证:△ADF∽△DEC;
(2)若AB=8,AD=6
| 3 |
| 3 |
考点:平行四边形的性质,相似三角形的判定与性质
专题:
分析:(1)易证∠ADF=∠CED和∠AFD=DCE,即可证明△ADF∽△DEC;
(2)根据平行四边形对边相等可求得CD的长,根据△ADF∽△DEC可得
=
,即可求得DE的长,根据勾股定理可以求得AE的长,即可解题.
(2)根据平行四边形对边相等可求得CD的长,根据△ADF∽△DEC可得
| AF |
| CD |
| AD |
| DE |
解答:(1)证明:∵平行四边形ABCD中,AB∥CD,AD∥BC,
∴∠B+∠DCE=180°,∠ADF=∠CED,
∵∠B=∠AFE,∠AFD+∠AFE=180°,
∴∠AFD=DCE,
∴△ADF∽△DEC;
(2)解:∵四边形ABCD为平行四边形,
∴CD=AB,AD∥BC,
∴AE⊥AD,
∵△ADF∽△DEC,
∴
=
,即
=
,
∴DE=12,
∵在RT△ADE中,AE2=DE2-AD2,
∴AE=6,
∴sinB=
=
=
.
∴∠B+∠DCE=180°,∠ADF=∠CED,
∵∠B=∠AFE,∠AFD+∠AFE=180°,
∴∠AFD=DCE,
∴△ADF∽△DEC;
(2)解:∵四边形ABCD为平行四边形,
∴CD=AB,AD∥BC,
∴AE⊥AD,
∵△ADF∽△DEC,
∴
| AF |
| CD |
| AD |
| DE |
4
| ||
| 8 |
6
| ||
| DE |
∴DE=12,
∵在RT△ADE中,AE2=DE2-AD2,
∴AE=6,
∴sinB=
| AE |
| AB |
| 6 |
| 8 |
| 3 |
| 4 |
点评:本题考查了相似三角形的判定,考查了相似三角形对应边比例相等的性质,考查了平行四边形对边平行且相等的性质,本题中求证△ADF∽△DEC是解题的关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
单项式-
xy2的系数和次数分别为( )
| 3 |
| 2 |
A、-
| ||
B、
| ||
C、
| ||
D、-
|
已知
+|b-1|=0,那么(a+b)2014的值为( )
| a+2 |
| A、1 |
| B、-1 |
| C、-32014 |
| D、32014 |