题目内容
已知二次函数y=x2+mx+m-5.
(1)求证:不论m取何值时,抛物线总与x轴有两个交点;
(2)求当m取何值时,抛物线与x轴两交点都在原点的左侧.
(1)求证:不论m取何值时,抛物线总与x轴有两个交点;
(2)求当m取何值时,抛物线与x轴两交点都在原点的左侧.
考点:抛物线与x轴的交点
专题:
分析:(1)当y=0时,根据b2-4ac恒>0,可得方程有2个根,即可解题;
(2)根据韦达定理可得x1+x2=-
,x1x2=
,根据x1+x2<0,x1x2>0即可求得m的值,即可解题.
(2)根据韦达定理可得x1+x2=-
| b |
| a |
| c |
| a |
解答:解:(1)当y=0时,有x2+mx+m-5=0,
b2-4ac=m2-4m+20=m2-4m+16+4=(m-2)2+16>0,
∴方程x2+mx+m-5=0有2个根,
∴不论m取何值时,抛物线总与x轴有两个交点;
(2)∵x1+x2=-
=-m,
x1x2=
=m-5,
∴当x1+x2<0,x1x2>0时,抛物线与x轴两交点都在原点的左侧,
即-m<0,m-5>0,
即0<m<5时,抛物线与x轴两交点都在原点的左侧.
b2-4ac=m2-4m+20=m2-4m+16+4=(m-2)2+16>0,
∴方程x2+mx+m-5=0有2个根,
∴不论m取何值时,抛物线总与x轴有两个交点;
(2)∵x1+x2=-
| b |
| a |
x1x2=
| c |
| a |
∴当x1+x2<0,x1x2>0时,抛物线与x轴两交点都在原点的左侧,
即-m<0,m-5>0,
即0<m<5时,抛物线与x轴两交点都在原点的左侧.
点评:本题考查了韦达定理的运用,考查了一元二次方程的求解,考查了一元一次不等式的求解,本题中根据韦达定理求解是解题的关键.

练习册系列答案
相关题目
单项式-
xy2的系数和次数分别为( )
| 3 |
| 2 |
A、-
| ||
B、
| ||
C、
| ||
D、-
|
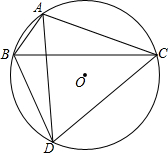 如图,△ABC内交于⊙O,∠BAC与平分线交⊙O于点D,若∠BAC=120°.
如图,△ABC内交于⊙O,∠BAC与平分线交⊙O于点D,若∠BAC=120°.
 如图,在△ABC中,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE于点E,AD⊥CE于点D.求证:
如图,在△ABC中,∠ACB=90°,AC=BC,AD⊥CE,BE⊥CE于点E,AD⊥CE于点D.求证: