题目内容
7．
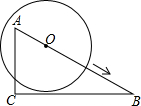如图，在Rt△ABC中，∠C=90°，∠B=30°，AC=3，⊙O在AB上由点A向点B运动，运动到圆心O与B点重合为止，⊙O的半径r=2，BO=m，则m取值范围如何时，⊙O与直线BC相交？相切？相离？
分析 若圆O与直线BC相切，则有OD=2，BO=x，求出x的值即可，若圆O与直线CB相离，则有OB大于x，若圆O与直线CB相交，则有OB小于x，可得到x的范围．
解答 
解：作OD∥AC，交BC于点D，
∵∠C=90°，∠B=30°，
∵BO=m，OD=2，
∴BO=2OD，
即m=4
即当m为4时，直线BC与⊙O相切；
若圆O与直线BC相离，则有OB大于m，
∵AC=3，
∴AB=6，4＜m≤6时，圆O与直线BC相离；
若圆O与直线CB相交，则有OB小于m，即0≤m＜4．
点评 此题考查了直线与圆的位置关系，直线与圆的位置关系由圆心到直线的距离d与圆的半径r的大小关系来判断．
练习册系列答案
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案
相关题目
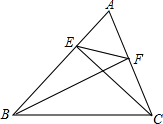如图，已知△ABC中，CE⊥AB于E，BE⊥AC于F，若S△ABC=36cm2，S△AEF=4cm2，求$\frac{EC}{AC}$的值．
在△ABC中，AB=10，∠C=100°，求△ABC外接圆⊙O的半径r．（用三角函数表示）
如图，用长为50米的篱笆囤成一个养鸡场，养鸡场的一面靠墙．问：（1）如何围，才能使养鸡场的面积最大？