题目内容
19. 如图,用长为50米的篱笆囤成一个养鸡场,养鸡场的一面靠墙.问:(1)如何围,才能使养鸡场的面积最大?
如图,用长为50米的篱笆囤成一个养鸡场,养鸡场的一面靠墙.问:(1)如何围,才能使养鸡场的面积最大?(2)若墙长只有20米,又如何围,才能使养鸡场的面积最大?
分析 (1)设长方形的宽为x米,表示出长,再根据长方形的面积公式列式整理,然后根据二次函数的最值问题解答即可.
(2)由于墙长只有20米,求出x的取值范围,根据二次函数性质解决问题.
解答 解:(1)设长方形的宽为x米,长方形的面积为y平方米,则长为:(50-2x)米,根据题意得:
y=x(50-2x)=-2x2+50x=-2(x-12.5)2+312.5,
当x=12.5米时,长方形面积最大,
即长方形的宽为12.5米,长为25米时,才能使养鸡场的面积最大;
(2)∵墙长只有20米,
∴50-2x≤20,
解得:x≥15
∴15≤x<25,
由于y=-2(x-12.5)2+312.5,
∵a=-2<0,
∴当x≥12.5时,y随x的增大而减小,
∴当x=15时,长方形的面积最大,
y=-2(15-12.5)2+312.5=300,
当鸡场的宽为15米,长为20米时,养鸡场的面积最大.
点评 本题考查了二次函数实际应用,列出函数表达式并熟练掌握二次函数的性质是解题的关键,把函数解析式整理成顶点式形式求解更简便.

练习册系列答案
相关题目
8.设a=$\sqrt{{4}^{2}}$,则a3-a2=( )
| A. | 2 | B. | 48 | C. | 6 | D. | 8 |
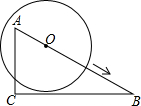 如图,在Rt△ABC中,∠C=90°,∠B=30°,AC=3,⊙O在AB上由点A向点B运动,运动到圆心O与B点重合为止,⊙O的半径r=2,BO=m,则m取值范围如何时,⊙O与直线BC相交?相切?相离?
如图,在Rt△ABC中,∠C=90°,∠B=30°,AC=3,⊙O在AB上由点A向点B运动,运动到圆心O与B点重合为止,⊙O的半径r=2,BO=m,则m取值范围如何时,⊙O与直线BC相交?相切?相离?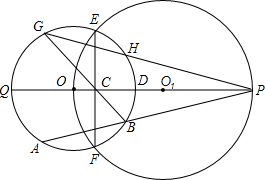 如图,⊙O1经过⊙O的圆心,E、F是两圆的交点,直线OO1交⊙O于点Q、D,交⊙O1于点P,交EF于点C,点A在劣弧QF上运动(与点Q、F不重合),连结PA交弧DF于B,连结BC并延长交⊙O于点G,连结PG交⊙O于点H.求证:
如图,⊙O1经过⊙O的圆心,E、F是两圆的交点,直线OO1交⊙O于点Q、D,交⊙O1于点P,交EF于点C,点A在劣弧QF上运动(与点Q、F不重合),连结PA交弧DF于B,连结BC并延长交⊙O于点G,连结PG交⊙O于点H.求证: 已知一次函数的图象经过点A(2,3),B(0,-2).
已知一次函数的图象经过点A(2,3),B(0,-2).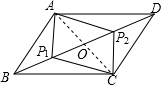 如图所示,在平行四边形ABCD中,BP1=DP2,求证:四边形AP1CP2是平行四边形.
如图所示,在平行四边形ABCD中,BP1=DP2,求证:四边形AP1CP2是平行四边形.