题目内容
20.阅读材料并解答问题:与正三角形各边都相切的圆叫做正三角形的内切圆,与正四边形各边都相切的圆叫做正四边形的内切圆,…,与正n边形各边都相切的圆叫做正n边形的内切圆,设正n(n≥3)边形的面积为S正n边形,其内切圆的半径为r,试探索正n边形的面积.(结果可用三角函数表示)
如图①,当n=3时,设AB切圆O于点C,连结OC,OA,OB,∴OC⊥AB,OA=OB,∴$∠AOC=\frac{1}{2}AOB$,AB=2BC.
在Rt△AOC中,∵$∠AOC=\frac{1}{2}•\frac{{{{360}°}}}{3}={60°}$,OC=r,∴AC=r•tan60°,AB=2r•tan60°,∴${S_{△OAB}}=\frac{1}{2}•r•2rtan{60°}={r^2}tan{60°}$,∴${S_{正三角形}}=3{S_{△OAB}}=3{r^2}•tan{60°}$.
(1)如图②,当n=4时,仿照(1)中的方法和过程可求得:S正四边形=4r2;
(2)如图③,当n=5时,仿照(1)中的方法和过程求S正五边形;
(3)如图④,根据以上探索过程,请直接写出S正n边形=nr2tan$\frac{180°}{n}$.
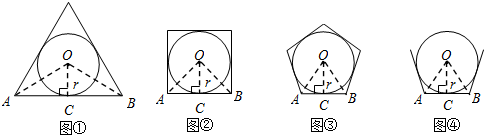
分析 (1)如图②,要求正四边形的面积,只需求△OAB的面积,只需求AB,根据等腰三角形的性质可得AB=2AC,只需在Rt△AOC中求出∠AOC,然后运用三角函数即可解决问题;
(2)如图③,要求正五边形的面积,只需求△OAB的面积,只需求AB,根据等腰三角形的性质可得AB=2AC,只需在Rt△AOC中求出∠AOC,然后运用三角函数即可解决问题;
(3)如图④,要求正n边形的面积,只需求△OAB的面积,只需求AB,根据等腰三角形的性质可得AB=2AC,只需在Rt△AOC中求出∠AOC,然后运用三角函数即可解决问题.
解答 解:(1)当n=4时,设AB切圆O于点C,连结OC、OA、OB,如图②,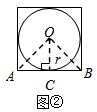
则有OC⊥AB,OA=OB,
∴∠AOC=$\frac{1}{2}$∠AOB,AB=2AC.
在Rt△AOC中,
∵∠AOC=$\frac{1}{2}$∠AOB=$\frac{1}{2}•$$\frac{360°}{4}$=45°,OC=r,
∴AC=r•tan45°,AB=2r•tan45°,
∴S△OAB=$\frac{1}{2}$•r•2r•tan45°=r2tan45°,
∴S正四边形=4S△OAB=4r2tan45°=4r2.
故答案为4r2;
(2)当n=5时,设AB切圆O于点C,连结OC、OA、OB,如图③,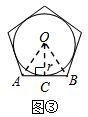
则有OC⊥AB,OA=OB,
∴∠AOC=$\frac{1}{2}$∠AOB,AB=2AC.
在Rt△AOC中,
∵∠AOC=$\frac{1}{2}$∠AOB=$\frac{1}{2}•$$\frac{360°}{5}$=36°,OC=r,
∴AC=r•tan36°,AB=2r•tan36°,
∴S△OAB=$\frac{1}{2}$•r•2r•tan36°=r2tan36°,
∴S正五边形=5S△OAB=5r2tan36°;
(3)设AB切圆O于点C,连结OC、OA、OB,如图④,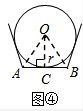
则有OC⊥AB,OA=OB,
∴∠AOC=$\frac{1}{2}$∠AOB,AB=2AC.
在Rt△AOC中,
∵∠AOC=$\frac{1}{2}$∠AOB=$\frac{1}{2}•$$\frac{360°}{n}$=$\frac{180°}{n}$,OC=r,
∴AC=r•tan$\frac{180°}{n}$,AB=2r•tan$\frac{180°}{n}$,
∴S△OAB=$\frac{1}{2}$•r•2r•tan$\frac{180°}{n}$=r2tan$\frac{180°}{n}$,
∴S正n边形=nS△OAB=nr2tan$\frac{180°}{n}$.
故答案为S正n边形=nr2tan$\frac{180°}{n}$.
点评 本题主要考查了正多边形和圆、锐角三角函数、切线的性质、等腰三角形的性质等知识,运用已有的经验解决问题是解决本题的关键.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案| A. | 2 | B. | 48 | C. | 6 | D. | 8 |
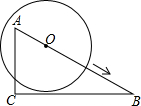 如图,在Rt△ABC中,∠C=90°,∠B=30°,AC=3,⊙O在AB上由点A向点B运动,运动到圆心O与B点重合为止,⊙O的半径r=2,BO=m,则m取值范围如何时,⊙O与直线BC相交?相切?相离?
如图,在Rt△ABC中,∠C=90°,∠B=30°,AC=3,⊙O在AB上由点A向点B运动,运动到圆心O与B点重合为止,⊙O的半径r=2,BO=m,则m取值范围如何时,⊙O与直线BC相交?相切?相离?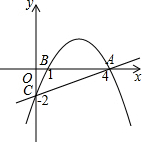 如图,抛物线经过A(4,0),B(1,0),C(0,-2)三点.
如图,抛物线经过A(4,0),B(1,0),C(0,-2)三点.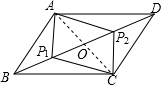 如图所示,在平行四边形ABCD中,BP1=DP2,求证:四边形AP1CP2是平行四边形.
如图所示,在平行四边形ABCD中,BP1=DP2,求证:四边形AP1CP2是平行四边形.