题目内容
18.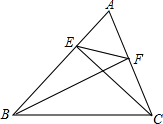 如图,已知△ABC中,CE⊥AB于E,BE⊥AC于F,若S△ABC=36cm2,S△AEF=4cm2,求$\frac{EC}{AC}$的值.
如图,已知△ABC中,CE⊥AB于E,BE⊥AC于F,若S△ABC=36cm2,S△AEF=4cm2,求$\frac{EC}{AC}$的值.
分析 由CE⊥AB,BF⊥AC,得到∠AEC=∠AFB=90°.推出△AFB∽△AEC,得到$\frac{AE}{AF}=\frac{AC}{AB}$,证得△AEF∽△ACB,求出$\frac{AC}{AE}$=$\sqrt{\frac{36}{4}}$=3,根据勾股定理得到CE=$\sqrt{A{C}^{2}-A{E}^{2}}$=2$\sqrt{2}$x,即可得到结论.
解答 证明:∵CE⊥AB,BF⊥AC,
∴∠AEC=∠AFB=90°.
∵∠A=∠A,
∴△AFB∽△AEC,
∴$\frac{AE}{AF}=\frac{AC}{AB}$,
即$\frac{AE}{AC}=\frac{AF}{AB}$,
∴△AEF∽△ACB,
∵S△ABC=36cm2,S△AEF=4cm2,∴$\frac{AC}{AE}$=$\sqrt{\frac{36}{4}}$=3,
假设AE=x,AC=3x,∴CE=$\sqrt{A{C}^{2}-A{E}^{2}}$=2$\sqrt{2}$x,
∴$\frac{EC}{AC}$=$\frac{2\sqrt{2}x}{3x}$=$\frac{2\sqrt{2}}{3}$.
点评 本题考查了相似三角形的判定和性质,垂直的定义,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
13.两个负数相乘的结果为6,这两个数不可能为( )
| A. | -12和$\frac{1}{2}$ | B. | -2和-3 | C. | -1和-6 | D. | -1和-6或-2和-3 |
 如图,把圆形纸片沿着一条弦CD翻折,使圆心O在折起的圆弧上,E,O分别是翻折前后的对应点,连接OE.求证:四边形CEDO是菱形.
如图,把圆形纸片沿着一条弦CD翻折,使圆心O在折起的圆弧上,E,O分别是翻折前后的对应点,连接OE.求证:四边形CEDO是菱形.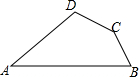 如图,在四边形ABCD中,∠A=30°,∠B=60°,AB=8,BC=2,AD=3$\sqrt{3}$.求四边形ABCD的面积.
如图,在四边形ABCD中,∠A=30°,∠B=60°,AB=8,BC=2,AD=3$\sqrt{3}$.求四边形ABCD的面积.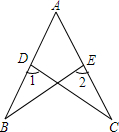 已知:如图,D、E分别是AB、AC上的点,AD=AE,∠1=∠2.求证:AB=AC.
已知:如图,D、E分别是AB、AC上的点,AD=AE,∠1=∠2.求证:AB=AC.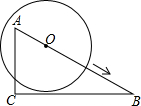 如图,在Rt△ABC中,∠C=90°,∠B=30°,AC=3,⊙O在AB上由点A向点B运动,运动到圆心O与B点重合为止,⊙O的半径r=2,BO=m,则m取值范围如何时,⊙O与直线BC相交?相切?相离?
如图,在Rt△ABC中,∠C=90°,∠B=30°,AC=3,⊙O在AB上由点A向点B运动,运动到圆心O与B点重合为止,⊙O的半径r=2,BO=m,则m取值范围如何时,⊙O与直线BC相交?相切?相离?