题目内容
2. 在△ABC中,AB=10,∠C=100°,求△ABC外接圆⊙O的半径r.(用三角函数表示)
在△ABC中,AB=10,∠C=100°,求△ABC外接圆⊙O的半径r.(用三角函数表示)
分析 作直径BD,连接AD,根据圆内接四边形的性质求出∠D的度数,根据圆周角定理得到∠DAB=90°,根据正弦的定义求出半径.
解答 解: 如图,作直径BD,连接AD,
如图,作直径BD,连接AD,
∵∠C=100°,
∴∠D=180°-100°=80°,
∵BD为直径,
∴∠DAB=90°,
又∵AB=10,
∴BD=$\frac{AB}{sin∠ADB}$=$\frac{10}{sin80°}$.
点评 本题考查的是三角形的外接圆和外心的概念以及锐角三角函数的概念,掌握直径所对的圆周角是直角、锐角三角函数的定义是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.一列数-3,-7,-11,-15…中第n个数为( )
| A. | n-4 | B. | -(2n+1) | C. | 4n-1 | D. | 1-4n |
13.两个负数相乘的结果为6,这两个数不可能为( )
| A. | -12和$\frac{1}{2}$ | B. | -2和-3 | C. | -1和-6 | D. | -1和-6或-2和-3 |
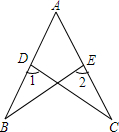 已知:如图,D、E分别是AB、AC上的点,AD=AE,∠1=∠2.求证:AB=AC.
已知:如图,D、E分别是AB、AC上的点,AD=AE,∠1=∠2.求证:AB=AC. 如图,△ABC中,∠BAC=90°,AD⊥BC于D,DE⊥AB于E,EF⊥BD于F.求证:CD:BD=DF:BF.
如图,△ABC中,∠BAC=90°,AD⊥BC于D,DE⊥AB于E,EF⊥BD于F.求证:CD:BD=DF:BF.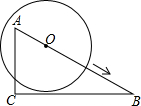 如图,在Rt△ABC中,∠C=90°,∠B=30°,AC=3,⊙O在AB上由点A向点B运动,运动到圆心O与B点重合为止,⊙O的半径r=2,BO=m,则m取值范围如何时,⊙O与直线BC相交?相切?相离?
如图,在Rt△ABC中,∠C=90°,∠B=30°,AC=3,⊙O在AB上由点A向点B运动,运动到圆心O与B点重合为止,⊙O的半径r=2,BO=m,则m取值范围如何时,⊙O与直线BC相交?相切?相离?