题目内容
15.一串数:$\frac{1}{1}$,-$\frac{1}{2}$,$\frac{2}{2}$,-$\frac{1}{2}$,$\frac{1}{3}$,-$\frac{2}{3}$,$\frac{3}{3}$,-$\frac{2}{3}$,$\frac{1}{3}$,-$\frac{1}{4}$,$\frac{2}{4}$,-$\frac{3}{4}$…试问:(1)$\frac{7}{11}$是第几个数?
(2)第400个数是多少?
分析 分母是1的分数有1个,分母是2的分数由3个,分母是3的分数有5个,…分母是n的分数有2n-1个分数;分子都是从1开始到与分母的数字相同连续的自然数,再倒数回到1,奇数位置为正,偶数位置为负,由此规律解决问题:
(1)首先算得到分母是10的分数一共有多少个分数,$\frac{7}{11}$在分母是11的分数中位于第7个和第15个数,由此得出答案即可;
(2)根据连续奇数和是数的个数的平方,可知第400个的分母是20,且是最后一个分数,由此得出答案即可.
解答 解:(1)到分母是10的分数一共有1+3+5+7+…+19=102=100(个),
$\frac{7}{11}$在分母是11的分数中位于第7个和第15个数,
所以$\frac{7}{11}$是第107个数和第115个数;
(2)∵400=202,
∴第400个的分母是20,且是最后一个分数为-$\frac{1}{20}$.
点评 此题考查数字的变化规律,找出数字之间的联系,得出规律,解决问题.

练习册系列答案
相关题目
8.设a=$\sqrt{{4}^{2}}$,则a3-a2=( )
| A. | 2 | B. | 48 | C. | 6 | D. | 8 |
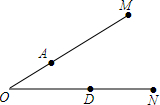 如图,角形铁架∠M0N小于60°,A,D分别是0M,0N上的点,为实际设计的需要,需在OM和0N上分别找出点C,B,使AB+BC+CD最短,问应如何找,并在图上表示出来.
如图,角形铁架∠M0N小于60°,A,D分别是0M,0N上的点,为实际设计的需要,需在OM和0N上分别找出点C,B,使AB+BC+CD最短,问应如何找,并在图上表示出来.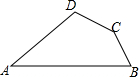 如图,在四边形ABCD中,∠A=30°,∠B=60°,AB=8,BC=2,AD=3$\sqrt{3}$.求四边形ABCD的面积.
如图,在四边形ABCD中,∠A=30°,∠B=60°,AB=8,BC=2,AD=3$\sqrt{3}$.求四边形ABCD的面积.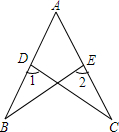 已知:如图,D、E分别是AB、AC上的点,AD=AE,∠1=∠2.求证:AB=AC.
已知:如图,D、E分别是AB、AC上的点,AD=AE,∠1=∠2.求证:AB=AC.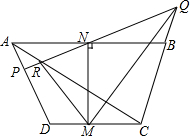 等腰梯形ABCD中,M和N分别为CD、AB的中点.过N作直线PQ和AD和CB的延长线分别交于P和Q,AC和PQ交于点R,求证:∠NMR=∠NMQ.
等腰梯形ABCD中,M和N分别为CD、AB的中点.过N作直线PQ和AD和CB的延长线分别交于P和Q,AC和PQ交于点R,求证:∠NMR=∠NMQ.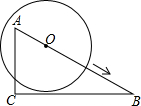 如图,在Rt△ABC中,∠C=90°,∠B=30°,AC=3,⊙O在AB上由点A向点B运动,运动到圆心O与B点重合为止,⊙O的半径r=2,BO=m,则m取值范围如何时,⊙O与直线BC相交?相切?相离?
如图,在Rt△ABC中,∠C=90°,∠B=30°,AC=3,⊙O在AB上由点A向点B运动,运动到圆心O与B点重合为止,⊙O的半径r=2,BO=m,则m取值范围如何时,⊙O与直线BC相交?相切?相离?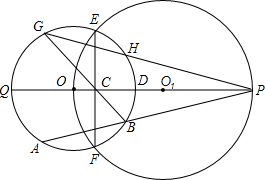 如图,⊙O1经过⊙O的圆心,E、F是两圆的交点,直线OO1交⊙O于点Q、D,交⊙O1于点P,交EF于点C,点A在劣弧QF上运动(与点Q、F不重合),连结PA交弧DF于B,连结BC并延长交⊙O于点G,连结PG交⊙O于点H.求证:
如图,⊙O1经过⊙O的圆心,E、F是两圆的交点,直线OO1交⊙O于点Q、D,交⊙O1于点P,交EF于点C,点A在劣弧QF上运动(与点Q、F不重合),连结PA交弧DF于B,连结BC并延长交⊙O于点G,连结PG交⊙O于点H.求证: