题目内容
3.化简:$\frac{{x}^{2}+2x+1}{{x}^{2}-1}$•$\frac{(x-1)^{2}}{x+1}$-x.分析 原式约分后,合并即可得到结果.
解答 解:原式=$\frac{(x+1)^{2}}{(x+1)(x-1)}$•$\frac{(x-1)^{2}}{x+1}$-x=x-1-x=-1.
点评 此题考查了分式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
13. 如图,已知AB∥CD,∠1=140°,则∠2=( )
如图,已知AB∥CD,∠1=140°,则∠2=( )
 如图,已知AB∥CD,∠1=140°,则∠2=( )
如图,已知AB∥CD,∠1=140°,则∠2=( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
14. 已知如图在Rt△ABC中,∠C=90°.CD是斜边AB上的高,若得到CD2=BD•AD这个结论可证明( )
已知如图在Rt△ABC中,∠C=90°.CD是斜边AB上的高,若得到CD2=BD•AD这个结论可证明( )
 已知如图在Rt△ABC中,∠C=90°.CD是斜边AB上的高,若得到CD2=BD•AD这个结论可证明( )
已知如图在Rt△ABC中,∠C=90°.CD是斜边AB上的高,若得到CD2=BD•AD这个结论可证明( )| A. | △ADC∽△ACB | B. | △BDC∽△BCA | C. | △ADC∽△CBD | D. | 无法判断 |
12. 如图,三直线两两相交于A、B、C,CA⊥CB,∠1=30°,则∠2的度数为( )
如图,三直线两两相交于A、B、C,CA⊥CB,∠1=30°,则∠2的度数为( )
 如图,三直线两两相交于A、B、C,CA⊥CB,∠1=30°,则∠2的度数为( )
如图,三直线两两相交于A、B、C,CA⊥CB,∠1=30°,则∠2的度数为( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
 如图,在平行四边形ABCD中,BE平分∠ABC,BC=6,DE=1,则平行四边形ABCD的周长等于22.
如图,在平行四边形ABCD中,BE平分∠ABC,BC=6,DE=1,则平行四边形ABCD的周长等于22.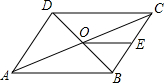 如图,在?ABCD中,对角线AC,BD交于点O,OE∥DC交BC于点E,若△BEO的面积为1,则?ABCD的面积等于8.
如图,在?ABCD中,对角线AC,BD交于点O,OE∥DC交BC于点E,若△BEO的面积为1,则?ABCD的面积等于8.