求不等式组$\left\{\begin{array}{l}{x-3≤2①}\\{1+\frac{1}{2}x＞2x②}\end{array}\right.$的正整数解．题目和参考答案——青夏教育精英家教网—

题目内容

11．求不等式组$\left\{\begin{array}{l}{x-3≤2①}\\{1+\frac{1}{2}x＞2x②}\end{array}\right.$的正整数解．

分析分别求出每个不等式的解集，根据：同小取小，确定不等式组的解集后即可得其正整数解的情况．

解答解：解不等式①，得：x≤5，
解不等式②，得：x＜$\frac{2}{3}$，
∴不等式组的解集为：x＜$\frac{2}{3}$，
∴不等式组不存在正整数解．

点评本题主要考查解不等式组的能力，熟练求出每个不等式的解集是解题根本，由口诀确定不等式组的解集是关键．

练习册系列答案

练习册吉林教育出版集团有限责任公司系列答案

练习册湖北教育出版社系列答案

新课标同步练习系列答案

实验作业系列答案

相关题目

1．

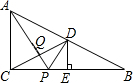如图，在Rt△ABC中，∠ACB=90°，点D是AB边的中点，过D作DE⊥BC于点E，点P是边BC上的一个动点，AP与CD相交于点Q．当AP+PD的值最小时，AQ与PQ之间的数量关系是（　　）

2．

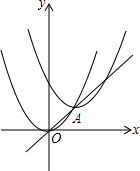如图，把抛物线y=x²沿直线y=x平移2$\sqrt{2}$个单位后，其顶点在直线上的A处，则平移后的抛物线解析式是（　　）

19．

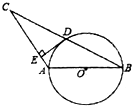如图，⊙O的直径AB=4，sin∠ABC=$\frac{1}{2}$，BC交⊙O于D，D是BC的中点．
（1）求BC的长；
（2）过点D作DE⊥AC，垂足为E，求证：直线DE是⊙O的切线．

6．为了解学生体育训练的情况，某市从全市九年级学生中随机抽取部分学生进行了一次体育科目测试（把测试结果分为四个等级：A级、B级、C级、D级），并将测试结果绘成了如下两幅不完整的统计图．请根据统计图中的信息解答下列问题：

（1）本次抽样测试的学生人数是400；
（2）扇形图中∠α的度数是108°，并把条形统计图补充完整；
（3）对A，B，C，D四个等级依次赋分为90，75，65，55（单位：分），比如：等级为A级的同学体育得分为90分，…，依此类推．该市九年级共有学生32000名，如果全部参加这次体育测试，则不及格（即60分以下）的有多少人？

16．

如图，点B、C在直线AD上，∠ABE=70°，BF平分∠DBE，CG∥BF，求∠DCG的度数．

3．化简：$\frac{{x}^{2}+2x+1}{{x}^{2}-1}$•$\frac{（x-1）^{2}}{x+1}$-x．

20．若（x+1）²+|y-1|=0，则x³+y¹⁰⁰¹=0．

1．已知点A（2-a，a+1）在第二象限，则a的取值范围是（　　）

试题分类