题目内容
13. 如图,已知AB∥CD,∠1=140°,则∠2=( )
如图,已知AB∥CD,∠1=140°,则∠2=( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
分析 根据对顶角相等求出∠3,再根据两直线平行,同旁内角互补求解.
解答  解:由对顶角相等得,∠3=∠1=140°,
解:由对顶角相等得,∠3=∠1=140°,
∵AB∥CD,
∴∠2=180°-∠3=180°-140°=40°.
故选B.
点评 本题考查了平行线的性质,熟记性质并准确识图理清图中各角度之间的关系是解题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
1.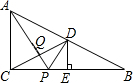 如图,在Rt△ABC中,∠ACB=90°,点D是AB边的中点,过D作DE⊥BC于点E,点P是边BC上的一个动点,AP与CD相交于点Q.当AP+PD的值最小时,AQ与PQ之间的数量关系是( )
如图,在Rt△ABC中,∠ACB=90°,点D是AB边的中点,过D作DE⊥BC于点E,点P是边BC上的一个动点,AP与CD相交于点Q.当AP+PD的值最小时,AQ与PQ之间的数量关系是( )
 如图,在Rt△ABC中,∠ACB=90°,点D是AB边的中点,过D作DE⊥BC于点E,点P是边BC上的一个动点,AP与CD相交于点Q.当AP+PD的值最小时,AQ与PQ之间的数量关系是( )
如图,在Rt△ABC中,∠ACB=90°,点D是AB边的中点,过D作DE⊥BC于点E,点P是边BC上的一个动点,AP与CD相交于点Q.当AP+PD的值最小时,AQ与PQ之间的数量关系是( )| A. | AQ=$\frac{5}{2}$PQ | B. | AQ=3PQ | C. | AQ=$\frac{8}{3}$PQ | D. | AQ=4PQ |
8.一种甲型H1N1流感病毒的直径约为0.00000078m,数0.00000078用科学记数法表示为( )
| A. | 0.78×10-5 | B. | 7.8×10-6 | C. | 7.8×10-7 | D. | 78×10-8 |
18.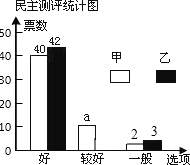 九年级一班邀请A、B、C、D、E五位评委对甲、乙两位同学的才艺表演打分,并组织全班50名同学对两人民意测评投费,绘制了如下的统计表和不完整的条形统计图:
九年级一班邀请A、B、C、D、E五位评委对甲、乙两位同学的才艺表演打分,并组织全班50名同学对两人民意测评投费,绘制了如下的统计表和不完整的条形统计图:
五位评委的打分表
并求得了五位评委对甲同学才艺表演所打分数的平均分和中位数:
$\overline{{x}_{甲}}$=$\frac{89+91+93+94+86}{5}$=90.6(分);中位数是91分.
(1)求五位评委对乙同学才艺表演所打分数的平均分和中位数;
(2)a=8,并补全条形统计图:
(3)为了从甲、乙二人中只选拔出一人去参加艺术节演出,班级制定了如下的选拔规则:

①当k=0.6时,通过计算说明应选拔哪位同学去参加艺术节演出?
②通过计算说明k的值不能是多少?
 九年级一班邀请A、B、C、D、E五位评委对甲、乙两位同学的才艺表演打分,并组织全班50名同学对两人民意测评投费,绘制了如下的统计表和不完整的条形统计图:
九年级一班邀请A、B、C、D、E五位评委对甲、乙两位同学的才艺表演打分,并组织全班50名同学对两人民意测评投费,绘制了如下的统计表和不完整的条形统计图:五位评委的打分表
| A | B | C | D | E | |
| 甲 | 89 | 91 | 93 | 94 | 86 |
| 乙 | 88 | 87 | 90 | 98 | 92 |
$\overline{{x}_{甲}}$=$\frac{89+91+93+94+86}{5}$=90.6(分);中位数是91分.
(1)求五位评委对乙同学才艺表演所打分数的平均分和中位数;
(2)a=8,并补全条形统计图:
(3)为了从甲、乙二人中只选拔出一人去参加艺术节演出,班级制定了如下的选拔规则:

①当k=0.6时,通过计算说明应选拔哪位同学去参加艺术节演出?
②通过计算说明k的值不能是多少?
5.关于x的方程x2-4x+4a=0有两个实数根,则a的取值范围是( )
| A. | a<1 | B. | a>1 | C. | a≤1 | D. | a≥1 |
2.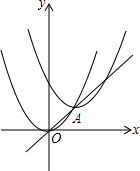 如图,把抛物线y=x2沿直线y=x平移2$\sqrt{2}$个单位后,其顶点在直线上的A处,则平移后的抛物线解析式是( )
如图,把抛物线y=x2沿直线y=x平移2$\sqrt{2}$个单位后,其顶点在直线上的A处,则平移后的抛物线解析式是( )
 如图,把抛物线y=x2沿直线y=x平移2$\sqrt{2}$个单位后,其顶点在直线上的A处,则平移后的抛物线解析式是( )
如图,把抛物线y=x2沿直线y=x平移2$\sqrt{2}$个单位后,其顶点在直线上的A处,则平移后的抛物线解析式是( )| A. | y=(x+2)2-2 | B. | y=(x+2)2+2 | C. | y=(x-2)2+2 | D. | y=(x-2)2-2 |
 如图,在△ABC中,∠BAC=106°,MP,NQ分别垂直平分AB,AC.
如图,在△ABC中,∠BAC=106°,MP,NQ分别垂直平分AB,AC.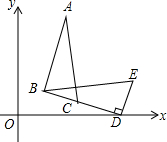 如图,在△BDE中,∠BDE=90°,BD=4$\sqrt{2}$,点D的坐标是(5,0),∠BDO=15°,将△BDE旋转得到△ABC的位置,点C在BD上,则过A、B、D三点圆的圆心坐标为(3,2$\sqrt{3}$).
如图,在△BDE中,∠BDE=90°,BD=4$\sqrt{2}$,点D的坐标是(5,0),∠BDO=15°,将△BDE旋转得到△ABC的位置,点C在BD上,则过A、B、D三点圆的圆心坐标为(3,2$\sqrt{3}$).