题目内容
8.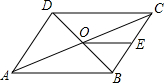 如图,在?ABCD中,对角线AC,BD交于点O,OE∥DC交BC于点E,若△BEO的面积为1,则?ABCD的面积等于8.
如图,在?ABCD中,对角线AC,BD交于点O,OE∥DC交BC于点E,若△BEO的面积为1,则?ABCD的面积等于8.
分析 由平行四边形的性质和相似三角形的性质得出△BCD的面积=4△BEO的面积=4,即可得出?ABCD的面积.
解答 解:∵四边形ABCD是平行四边形,
∴OA=OC=$\frac{1}{2}$AC,BCD的面积=$\frac{1}{2}$四边形ABCD的面积,
∵OE∥DC,
∴△BEO∽△BCD,
∴△BEO的面积:△BCD的面积=1:4,
∴△BCD的面积=4△BEO的面积=4×1=4,
∴?ABCD的面积=4×2=8;
故答案为:8.
点评 本题考查了平行四边形的性质、相似三角形的判定与性质;熟练掌握平行四边形的性质,证明三角形相似是解决问题的个关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.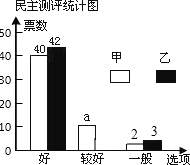 九年级一班邀请A、B、C、D、E五位评委对甲、乙两位同学的才艺表演打分,并组织全班50名同学对两人民意测评投费,绘制了如下的统计表和不完整的条形统计图:
九年级一班邀请A、B、C、D、E五位评委对甲、乙两位同学的才艺表演打分,并组织全班50名同学对两人民意测评投费,绘制了如下的统计表和不完整的条形统计图:
五位评委的打分表
并求得了五位评委对甲同学才艺表演所打分数的平均分和中位数:
$\overline{{x}_{甲}}$=$\frac{89+91+93+94+86}{5}$=90.6(分);中位数是91分.
(1)求五位评委对乙同学才艺表演所打分数的平均分和中位数;
(2)a=8,并补全条形统计图:
(3)为了从甲、乙二人中只选拔出一人去参加艺术节演出,班级制定了如下的选拔规则:

①当k=0.6时,通过计算说明应选拔哪位同学去参加艺术节演出?
②通过计算说明k的值不能是多少?
 九年级一班邀请A、B、C、D、E五位评委对甲、乙两位同学的才艺表演打分,并组织全班50名同学对两人民意测评投费,绘制了如下的统计表和不完整的条形统计图:
九年级一班邀请A、B、C、D、E五位评委对甲、乙两位同学的才艺表演打分,并组织全班50名同学对两人民意测评投费,绘制了如下的统计表和不完整的条形统计图:五位评委的打分表
| A | B | C | D | E | |
| 甲 | 89 | 91 | 93 | 94 | 86 |
| 乙 | 88 | 87 | 90 | 98 | 92 |
$\overline{{x}_{甲}}$=$\frac{89+91+93+94+86}{5}$=90.6(分);中位数是91分.
(1)求五位评委对乙同学才艺表演所打分数的平均分和中位数;
(2)a=8,并补全条形统计图:
(3)为了从甲、乙二人中只选拔出一人去参加艺术节演出,班级制定了如下的选拔规则:

①当k=0.6时,通过计算说明应选拔哪位同学去参加艺术节演出?
②通过计算说明k的值不能是多少?
13.据统计,2015年我国手机上网人数约为6.20亿,数据6.20亿用科学记数法表示为( )
| A. | 0.620×1011 | B. | 6.20×1010 | C. | 6.20×109 | D. | 6.20×108 |
15.如图1,是装有三个小轮的手拉车在“爬”楼梯时的侧面示意图,定长的轮架杆OA,OB,OC抽象为线段,有OA=OB=OC,且∠AOB=120°.折线NG-GH-HE-EF表示楼梯,GH,EF是水平线,NG,HE是铅垂线,半径相等的小轮子⊙A,⊙B与楼梯两边都相切,且AO∥GH.如图2,若点H在线段OB时,则$\frac{BH}{OH}$的值是( )
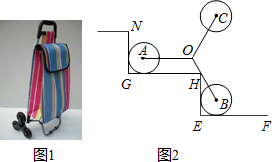

| A. | $\frac{1}{2}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
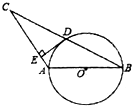 如图,⊙O的直径AB=4,sin∠ABC=$\frac{1}{2}$,BC交⊙O于D,D是BC的中点.
如图,⊙O的直径AB=4,sin∠ABC=$\frac{1}{2}$,BC交⊙O于D,D是BC的中点. 如图,点B、C在直线AD上,∠ABE=70°,BF平分∠DBE,CG∥BF,求∠DCG的度数.
如图,点B、C在直线AD上,∠ABE=70°,BF平分∠DBE,CG∥BF,求∠DCG的度数. 如图,矩形OABC的边OA在x轴上,双曲线y=$\frac{k}{x}$与BC交于点D,与AB交于点E,DE=$\frac{1}{2}$OB,矩形OABC的面积为4,则k的值为2.
如图,矩形OABC的边OA在x轴上,双曲线y=$\frac{k}{x}$与BC交于点D,与AB交于点E,DE=$\frac{1}{2}$OB,矩形OABC的面积为4,则k的值为2.