题目内容
14. 已知如图在Rt△ABC中,∠C=90°.CD是斜边AB上的高,若得到CD2=BD•AD这个结论可证明( )
已知如图在Rt△ABC中,∠C=90°.CD是斜边AB上的高,若得到CD2=BD•AD这个结论可证明( )| A. | △ADC∽△ACB | B. | △BDC∽△BCA | C. | △ADC∽△CBD | D. | 无法判断 |
分析 根据三角形内角和定理和已知求出∠B=∠ACD,根据相似三角形的判定得出△ADC∽△CDB,根据相似三角形的性质得出比例式,即可得出选项.
解答 解:△ADC∽△CBD,
理由是:∵在Rt△ABC中,∠C=90°.CD是斜边AB上的高,
∴∠ACB=∠CDB=∠CDA=90°,
∴∠B+∠BCD=90°,∠BCD+∠ACD=90°,
∴∠B=∠ACD,
∵∠CDB=∠ADC=90°,
∴△ADC∽△CDB,
∴$\frac{CD}{BD}$=$\frac{AD}{CD}$,
∴CD2=BD•AD,即只有选项C正确;选项A、B、D都错误;
故选C.
点评 本题考查了相似三角形的性质和判定的应用,能灵活运用定理进行推理是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.关于x的方程x2-4x+4a=0有两个实数根,则a的取值范围是( )
| A. | a<1 | B. | a>1 | C. | a≤1 | D. | a≥1 |
2.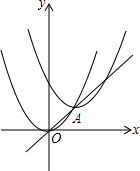 如图,把抛物线y=x2沿直线y=x平移2$\sqrt{2}$个单位后,其顶点在直线上的A处,则平移后的抛物线解析式是( )
如图,把抛物线y=x2沿直线y=x平移2$\sqrt{2}$个单位后,其顶点在直线上的A处,则平移后的抛物线解析式是( )
 如图,把抛物线y=x2沿直线y=x平移2$\sqrt{2}$个单位后,其顶点在直线上的A处,则平移后的抛物线解析式是( )
如图,把抛物线y=x2沿直线y=x平移2$\sqrt{2}$个单位后,其顶点在直线上的A处,则平移后的抛物线解析式是( )| A. | y=(x+2)2-2 | B. | y=(x+2)2+2 | C. | y=(x-2)2+2 | D. | y=(x-2)2-2 |
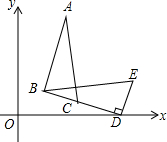 如图,在△BDE中,∠BDE=90°,BD=4$\sqrt{2}$,点D的坐标是(5,0),∠BDO=15°,将△BDE旋转得到△ABC的位置,点C在BD上,则过A、B、D三点圆的圆心坐标为(3,2$\sqrt{3}$).
如图,在△BDE中,∠BDE=90°,BD=4$\sqrt{2}$,点D的坐标是(5,0),∠BDO=15°,将△BDE旋转得到△ABC的位置,点C在BD上,则过A、B、D三点圆的圆心坐标为(3,2$\sqrt{3}$).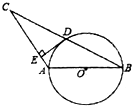 如图,⊙O的直径AB=4,sin∠ABC=$\frac{1}{2}$,BC交⊙O于D,D是BC的中点.
如图,⊙O的直径AB=4,sin∠ABC=$\frac{1}{2}$,BC交⊙O于D,D是BC的中点.