题目内容
12. 如图,三直线两两相交于A、B、C,CA⊥CB,∠1=30°,则∠2的度数为( )
如图,三直线两两相交于A、B、C,CA⊥CB,∠1=30°,则∠2的度数为( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
分析 根据垂直的定义得到∠ACB=90°,然后根据三角形的内角和即可得到结论.
解答 解:∵CA⊥CB,
∴∠ACB=90°,
∴∠2=180°-∠ACB-∠1=180°-90°-30°=60°,
故选B.
点评 本题考查了三角形内角和和垂直的定义,熟记三角形的内角和定理是解题的关键.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
2.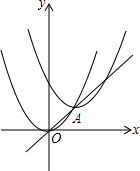 如图,把抛物线y=x2沿直线y=x平移2$\sqrt{2}$个单位后,其顶点在直线上的A处,则平移后的抛物线解析式是( )
如图,把抛物线y=x2沿直线y=x平移2$\sqrt{2}$个单位后,其顶点在直线上的A处,则平移后的抛物线解析式是( )
 如图,把抛物线y=x2沿直线y=x平移2$\sqrt{2}$个单位后,其顶点在直线上的A处,则平移后的抛物线解析式是( )
如图,把抛物线y=x2沿直线y=x平移2$\sqrt{2}$个单位后,其顶点在直线上的A处,则平移后的抛物线解析式是( )| A. | y=(x+2)2-2 | B. | y=(x+2)2+2 | C. | y=(x-2)2+2 | D. | y=(x-2)2-2 |
1.已知点A(2-a,a+1)在第二象限,则a的取值范围是( )
| A. | a>2 | B. | -1<a<2 | C. | a<-1 | D. | a<1 |
 如图,矩形OABC的边OA在x轴上,双曲线y=$\frac{k}{x}$与BC交于点D,与AB交于点E,DE=$\frac{1}{2}$OB,矩形OABC的面积为4,则k的值为2.
如图,矩形OABC的边OA在x轴上,双曲线y=$\frac{k}{x}$与BC交于点D,与AB交于点E,DE=$\frac{1}{2}$OB,矩形OABC的面积为4,则k的值为2.