题目内容
10.已知a,b为实数,且$\sqrt{1+a}$-(b-1)$\sqrt{1-b}$=0,求a2015-b2016的值.分析 由已知条件得到$\sqrt{1+a}$+(1-b)$\sqrt{1-b}$=0,利用二次根式有意义的条件得到1-b≥0,再根据几个非负数和的性质得到1+a=0,1-b=0,解得a=-1,b=1,然后根据乘方的意义计算a2015-b2016的值.
解答 解:∵$\sqrt{1+a}$-(b-1)$\sqrt{1-b}$=0,
∴$\sqrt{1+a}$+(1-b)$\sqrt{1-b}$=0,
∵1-b≥0,
∴1+a=0,1-b=0,解得a=-1,b=1,
∴a2015-b2016=(-1)2015-12016=-1-1=-2.
点评 本题考查了非负数的性质:算术平方根具有非负性.非负数之和等于0时,各项都等于0利用此性质列方程解决求值问题.

练习册系列答案
相关题目
1.已知点A(2-a,a+1)在第二象限,则a的取值范围是( )
| A. | a>2 | B. | -1<a<2 | C. | a<-1 | D. | a<1 |
15.如图1,是装有三个小轮的手拉车在“爬”楼梯时的侧面示意图,定长的轮架杆OA,OB,OC抽象为线段,有OA=OB=OC,且∠AOB=120°.折线NG-GH-HE-EF表示楼梯,GH,EF是水平线,NG,HE是铅垂线,半径相等的小轮子⊙A,⊙B与楼梯两边都相切,且AO∥GH.如图2,若点H在线段OB时,则$\frac{BH}{OH}$的值是( )
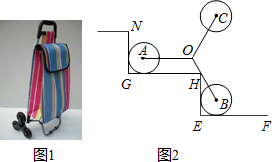

| A. | $\frac{1}{2}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
