题目内容
6.关于x的一元二次方程x2+(2k+1)x+k2+1=0有两个不相等的实数根x1、x2.(1)求实数k的取值范围;
(2)若x1+x2=x1•x2,求k的值.
分析 (1)由方程的系数结合根的判别式即可得出关于k的一元一次不等式,解之即可得出实数k的取值范围;
(2)由根与系数的关系可得x1+x2=-(2k+1)、x1•x2=k2+1,结合x1+x2=x1•x2即可得出关于k的一元二次方程,解之即可得出k值,再根据k>$\frac{3}{4}$即可确定k的值.
解答 解:(1)∵关于x的一元二次方程x2+(2k+1)x+k2+1=0有两个不相等的实数根,
∴△=(2k+1)2-4(k2+1)=4k-3>0,
解得:k>$\frac{3}{4}$.
∴实数k的取值范围为k>$\frac{3}{4}$.
(2)由根与系数的关系,得:x1+x2=-(2k+1),x1•x2=k2+1,
∵x1+x2=x1•x2,
∴-(2k+1)=k2+1,
方程无解.
点评 本题考查了根与系数的关系、根的判别式以及解一元二次方程,根据根与系数的关系得出关于k的一元二次方程是解题的关键.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
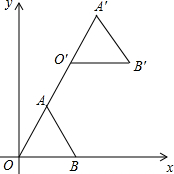 已知:如图,在平面直角坐标系中,正三角形OAB的顶点B的坐标为(2,0),点A在第一象限内
已知:如图,在平面直角坐标系中,正三角形OAB的顶点B的坐标为(2,0),点A在第一象限内