Question

1．如图是由非负偶数排成的数阵：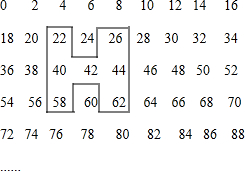

（1）写出图中“H”形框中七个数的和与中间数的关系；
（2）在数阵中任意做一个这样的“H”形框，（1）中的关系是否仍成立？并写出理由；
（3）用这样的“H”形框能框出和为2023的七个数吗？如果能，求出这七个数中间的数；如果不能，请写出理由．

Answer 1

分析 （1）将7个数相加即可得；
（2）设中间数为x，则其余六个数分别为x-2，x+2，x-20，x+20，x-16，x+16，将7个数相加即可得出关系；
（3）由2023÷7=289，且数列是非负偶数数阵，而289是奇数可得答案．

解答 解：（1）∵22+40+58+42+26+44+62=294=7×42，
∴图中“H”形框中七个数的和是中间数的7倍；

（2）成立，
设中间数为x，则其余六个数分别为x-2，x+2，x-20，x+20，x-16，x+16，
∴x-2+x+2+x-20+x+20+x-16+x+16=7x，
所以图中“H”形框中七个数的和是中间数的7倍；

（3）不能，
2023÷7=289，
∵是非负偶数数阵，而289是奇数，
∴不能框出和为2023的七个数．

点评 本题主要考查数字的变化规律，根据题意用x表示出每个数是解题的关键．