题目内容
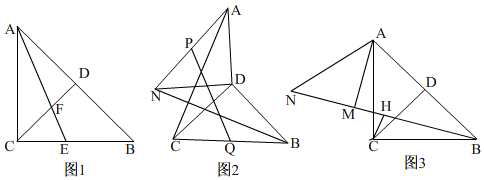
11.如图,在等腰直角△ABC中,∠ACB=90°,CA=CB,CD为斜边AB上的中线.(1)如图1,AE平分∠CAB交BC于E,交CD于F,若DF=2,求AC的长;
(2)将图1中的△ADC绕点D顺时针旋转一定角度得到△ADN,如图2,P,Q分别为线段AN,BC的中点,连接AC,BN,PQ,求证:BN=$\sqrt{2}$PQ;
(3)如图3,将△ADC绕点A顺时针旋转一定角度到△AMN,其中D的对应点是M,C的对应点是N,若B,M,N三点在同一直线上,H为BN中点,连接CH,猜想BM,MN,CH之间的数量关系,请直接写出结果.
分析 (1)利用角平分线定理求出FM,再利用等腰直角三角形的性质即可得出CF,最后用AC=$\sqrt{2}$CD即可;
(2)先判断出$\frac{DN}{DP}=\frac{DB}{DQ}$=$\sqrt{2}$,再判断出∠PDQ=∠NDB,进而得出,△PDQ∽△NDB即可判断出结论;
(3)先判断出,∠MAC=∠GBC进而得出△ACM≌△BCG,即可得出∠ACM=∠BCG,进而△MCG是直角三角形,再用直角三角形的中线得出MG=2CH,最后等量代换即可.
解答 解:(1)如图1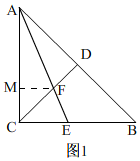 ∵等腰直角△ABC中,∠ACB=90°,CA=CB,CD为斜边AB上的中线.
∵等腰直角△ABC中,∠ACB=90°,CA=CB,CD为斜边AB上的中线.
∴CD⊥AB,∠ACD=45°
过点F作FM⊥AC,
∵AE平分∠CAB,
∴FM=FD=2
在Rt△CMF中,∠ACD=45°,
∴CF=$\sqrt{2}$MF=2$\sqrt{2}$,
∴CD=CF+FD=2$\sqrt{2}$+2,
∵CD是等腰直角三角形斜边的中线,
∴AC=$\sqrt{2}$CD=$\sqrt{2}$(2$\sqrt{2}$+2)=4+2$\sqrt{2}$;
(2)如图2,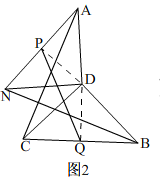 连接DP,DQ,
连接DP,DQ,
∵△ADC绕点D顺时针旋转一定角度得到△ADN,
∴AN=BC,DN=CD=DB,△ADN是等腰直角三角形,
∵△BCD是等腰直角三角形,点Q是BC中点,
∴DQ=$\frac{1}{2}$BC=$\frac{1}{2}$×$\sqrt{2}$BD=$\frac{\sqrt{2}}{2}$DN,
∵点P是AN中点,
∴DP=$\frac{1}{2}$AN=$\frac{1}{2}$BC=DQ,
∴$\frac{DN}{DP}=\frac{DB}{DQ}$=$\sqrt{2}$,
∵∠NDP=∠CDQ=45°,
∴∠PDQ=∠PDN+∠CDN+∠CDQ=90°+∠CDN,
∵∠NDB=∠CDN+∠CDB=90°+∠CDN,
∴∠PDQ=∠NDB,
∵$\frac{DN}{DP}=\frac{DB}{DQ}$=$\sqrt{2}$,
∴△PDQ∽△NDB,
∴$\frac{BN}{PQ}=\frac{DN}{DP}$=$\sqrt{2}$,
∴BN=$\sqrt{2}$PQ.
(3)BM-MN=2CH.
理由:如图3, 在BN上截取BG=BD,连接CG,CM,
在BN上截取BG=BD,连接CG,CM,
∵△ADC绕点A顺时针旋转一定角度到△AMN,
∴MN=AM=AD=CD=DB,
∴MN=AM=BG,
根据三角形的内角和,得∠MAC=∠GBC,
在△ACM和△BCG中,$\left\{\begin{array}{l}{AC=BC}\\{∠MAC=∠GBC}\\{AM=BG}\end{array}\right.$,
∴△ACM≌△BCG,
∴∠ACM=∠BCG,
∴∠MCG=∠ACM+∠ACG=∠BCG+∠ACG=90°,
∴△MCG是直角三角形,
∵H为BN中点,
∴BH=NH,
∵BG=MN,
∴HG=HM,
在Rt△MCG中,HG=HM,
∴MG=2CH,
∴BM=BG+MG=MN+2CH,
∴BM-MN=2CH.
点评 此题是三角形综合题,主要考查了等腰直角三角形的性质,全等三角形的判定和性质,相似三角形的判定和性质,旋转的性质,直角三角形的判定等知识点,解本题的关键是判断出△PDQ∽△NDB和△MCG是直角三角形,作出辅助线是解本题的难点,是一道很好的中考压轴题.

 如图,AB是⊙O的直径,弦CD⊥AB于点E,AM是△ACD的外角∠DAF的平分线.
如图,AB是⊙O的直径,弦CD⊥AB于点E,AM是△ACD的外角∠DAF的平分线.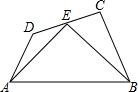 如图,在四边形ABCD中,∠BCD=90°,E为CD的中点,连接AE、BE,AE=BE,AE⊥BE,若BC-CD=2,AD=$\sqrt{74}$,则AB边的长为13$\sqrt{2}$.
如图,在四边形ABCD中,∠BCD=90°,E为CD的中点,连接AE、BE,AE=BE,AE⊥BE,若BC-CD=2,AD=$\sqrt{74}$,则AB边的长为13$\sqrt{2}$.