题目内容
14.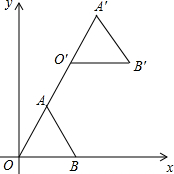 已知:如图,在平面直角坐标系中,正三角形OAB的顶点B的坐标为(2,0),点A在第一象限内
已知:如图,在平面直角坐标系中,正三角形OAB的顶点B的坐标为(2,0),点A在第一象限内(1)求点A的坐标
(2)如图,将△OAB沿O到A的方向平移4个单位至△O′A′B′的位置,即AA′=4,求点B′的坐标
(3)如图,将△OAB沿O到A的方向平移n个单位至△O′A′B′的位置,若平移后的B′点横坐标为2017,求n的值.
分析 (1)作AM⊥x轴于点M.根据等边三角形的性质得出OA=OB=2,∠AOB=60°,在直角△OAM中利用含30°角的直角三角形的性质求出OM=$\frac{1}{2}$OA=1,AM=$\sqrt{3}$OM=$\sqrt{3}$,则A的坐标可求;
(2)根据平移的性质可知当AA′=4时,OO′=4,连结O′B,由OA=O′A=AB=2,得出∠O′BO=90°,再解直角△OO′B,得出OB=$\frac{1}{2}$OO′=2,O′B=$\sqrt{3}$OB=2$\sqrt{3}$,进而求出点B′的坐标;
(3)过O′作x轴的垂线,垂足为P.解直角△OO′P,得出OP=$\frac{1}{2}$OO′=$\frac{1}{2}$n,根据平移后的B′点横坐标为2017,列出方程$\frac{1}{2}$n+2=2017,求解即可.
解答 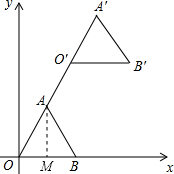 解:(1)如图,作AM⊥x轴于点M.
解:(1)如图,作AM⊥x轴于点M.
∵正三角形OAB的顶点B的坐标为(2,0),
∴OA=OB=2,∠AOB=60°,
∴OM=$\frac{1}{2}$OA=1,AM=$\sqrt{3}$OM=$\sqrt{3}$,
∴A(1,$\sqrt{3}$);
(2)当AA′=4时,OO′=4,连结O′B,如图,
∵OA=O′A=AB=2,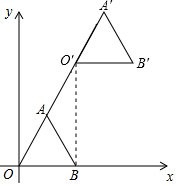 ∴∠O′BO=90°,
∴∠O′BO=90°,
∴OB=$\frac{1}{2}$OO′=2,O′B=$\sqrt{3}$OB=2$\sqrt{3}$,
∴点B′的坐标为(2+2,2$\sqrt{3}$),即(4,2$\sqrt{3}$);
(3)如图,将△OAB沿O到A的方向平移n个单位至△O′A′B′的位置,即AA′=n,
∴OO′=n.
如下图,过O′作x轴的垂线,垂足为P.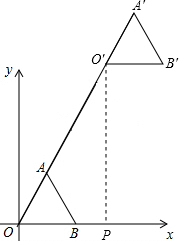
在△OO′P中,∵∠O′PO=90°,∠OO′P=30°,OO′=n,
∴OP=$\frac{1}{2}$OO′=$\frac{1}{2}$n,
∵平移后的B′点横坐标为2017,O′B′=2,
∴$\frac{1}{2}$n+2=2017,
∴n=4030.
点评 本题考查了坐标与图形变化-平移,在平面直角坐标系中,图形的平移与图形上某点的平移相同.平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.也考查了等边三角形的性质,含30°角的直角三角形的性质.求出OB′的长度是解题的关键.

 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案 如图,AB是⊙O的直径,弦CD⊥AB于点E,AM是△ACD的外角∠DAF的平分线.
如图,AB是⊙O的直径,弦CD⊥AB于点E,AM是△ACD的外角∠DAF的平分线.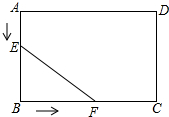 如图,在矩形ABCD中,AB=5cm,BC=7cm,点E从点A出发,沿AB方向以1cm/s的速度向点B移动,同时,点F从点B出发,沿BC方向以2cm/s的速度向点C移动,当点F到达点C时,两点同时停止运动,设运动时间为t秒.
如图,在矩形ABCD中,AB=5cm,BC=7cm,点E从点A出发,沿AB方向以1cm/s的速度向点B移动,同时,点F从点B出发,沿BC方向以2cm/s的速度向点C移动,当点F到达点C时,两点同时停止运动,设运动时间为t秒.