题目内容
7.有一列按一定顺序和规律排列的数:第一个数是$\frac{1}{1×2}$;
第二个数是$\frac{1}{2×3}$;
第三个数是$\frac{1}{3×4}$;
…
对任何正整数n,第n个数与第(n+1)个数的和等于$\frac{2}{n×(n+2)}$.
(1)经过探究,我们发现:$\frac{1}{1×2}=\frac{1}{1}-\frac{1}{2}$,$\frac{1}{2×3}=\frac{1}{2}-\frac{1}{3}$,$\frac{1}{3×4}=\frac{1}{3}-\frac{1}{4}$,
设这列数的第5个数为a,那么$a>\frac{1}{5}-\frac{1}{6}$,$a=\frac{1}{5}-\frac{1}{6}$,$a<\frac{1}{5}-\frac{1}{6}$,哪个正确?
请你直接写出正确的结论;
(2)请你观察第1个数、第2个数、第3个数,猜想这列数的第n个数(即用正整数n表示第n数),并且证明你的猜想满足“第n个数与第(n+1)个数的和等于$\frac{2}{n×(n+2)}$”;
(3)设M表示$\frac{1}{1^2}$,$\frac{1}{2^2}$,$\frac{1}{3^2}$,…,$\frac{1}{{{{2016}^2}}}$,这2016个数的和,即$M=\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+…\frac{1}{{{{2016}^2}}}$,
求证:$\frac{2016}{2017}<M<\frac{4031}{2016}$.
分析 (1)由已知规律可得;
(2)先根据已知规律写出第n、n+1个数,再根据分式的运算化简可得;
(3)将每个分式根据$\frac{1}{n}$-$\frac{1}{n+1}$=$\frac{1}{n(n+1)}$<$\frac{1}{{n}^{2}}$<$\frac{1}{n(n-1)}$=$\frac{1}{n-1}$-$\frac{1}{n}$,展开后再全部相加可得结论.
解答 解:(1)由题意知第5个数a=$\frac{1}{5×6}$=$\frac{1}{5}$-$\frac{1}{6}$;
(2)∵第n个数为$\frac{1}{n(n+1)}$,第(n+1)个数为$\frac{1}{(n+1)(n+2)}$,
∴$\frac{1}{n(n+1)}$+$\frac{1}{(n+1)(n+2)}$=$\frac{1}{n+1}$($\frac{1}{n}$+$\frac{1}{n+2}$)
=$\frac{1}{n+1}$×$\frac{n+2+n}{n(n+2)}$
=$\frac{1}{n+1}$×$\frac{2(n+1)}{n(n+2)}$
=$\frac{2}{n(n+2)}$,
即第n个数与第(n+1)个数的和等于$\frac{2}{n×(n+2)}$;
(3)∵1-$\frac{1}{2}$=$\frac{1}{1×2}$<$\frac{1}{{1}^{2}}$=1,
$\frac{1}{2}-$$\frac{1}{3}$=$\frac{1}{2×3}$<$\frac{1}{{2}^{2}}$<$\frac{1}{1×2}$=1-$\frac{1}{2}$,
$\frac{1}{3}$-$\frac{1}{4}$=$\frac{1}{3×4}$<$\frac{1}{{3}^{2}}$<$\frac{1}{2×3}$=$\frac{1}{2}$-$\frac{1}{3}$,
…
$\frac{1}{2015}$-$\frac{1}{2016}$=$\frac{1}{2015×2016}$<$\frac{1}{201{5}^{2}}$<$\frac{1}{2014×2015}$=$\frac{1}{2014}$-$\frac{1}{2015}$,
$\frac{1}{2016}$-$\frac{1}{2017}$=$\frac{1}{2016×2017}$<$\frac{1}{201{6}^{2}}$<$\frac{1}{2015×2016}$=$\frac{1}{2015}$-$\frac{1}{2016}$,
∴1-$\frac{1}{2017}$<$\frac{1}{1^2}$+$\frac{1}{2^2}$+$\frac{1}{3^2}$+…+$\frac{1}{201{5}^{2}}$+$\frac{1}{{{{2016}^2}}}$<2-$\frac{1}{2016}$,
即$\frac{2016}{2017}$<$\frac{1}{1^2}$+$\frac{1}{2^2}$+$\frac{1}{3^2}$+…+$\frac{1}{201{5}^{2}}$+$\frac{1}{{{{2016}^2}}}$<$\frac{4031}{2016}$,
∴$\frac{2016}{2017}<M<\frac{4031}{2016}$.
点评 本题主要考查分式的混合运算及数字的变化规律,根据已知规律$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$得到$\frac{1}{n}$-$\frac{1}{n+1}$=$\frac{1}{n(n+1)}$<$\frac{1}{{n}^{2}}$<$\frac{1}{n(n-1)}$=$\frac{1}{n-1}$-$\frac{1}{n}$是解题的关键.

| A. | y=-2x | B. | y=2x | C. | y=-$\frac{1}{2}$x | D. | y=$\frac{1}{2}$x |
| A. | a2×a5=a10 | B. | $\sqrt{a+b}=\sqrt{a}+\sqrt{b}$ | C. | (-a3)4=a12 | D. | $\sqrt{a^2}=a$ |
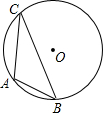 如图,已知⊙O的直径为8cm,A、B、C三点在⊙O上,且∠ACB=30°,则AB长为( )
如图,已知⊙O的直径为8cm,A、B、C三点在⊙O上,且∠ACB=30°,则AB长为( )| A. | 3cm | B. | 4cm | C. | 2$\sqrt{2}$cm | D. | 2$\sqrt{3}$cm |
| A. | $\sqrt{45}-2\sqrt{5}=\sqrt{5}$ | B. | (π-3.14)0=0 | C. | a2•a5=a10 | D. | (a+b)2=a2+b2 |
 如图,Rt△ABO的顶点O在坐标原点,点B在x轴上,∠ABO=90°,∠AOB=30°,OB=2$\sqrt{3}$,反比例函数y=$\frac{k}{x}$(x>0)的图象经过OA的中点C,交AB于点D.
如图,Rt△ABO的顶点O在坐标原点,点B在x轴上,∠ABO=90°,∠AOB=30°,OB=2$\sqrt{3}$,反比例函数y=$\frac{k}{x}$(x>0)的图象经过OA的中点C,交AB于点D.