题目内容
15. 如图,Rt△ABO的顶点O在坐标原点,点B在x轴上,∠ABO=90°,∠AOB=30°,OB=2$\sqrt{3}$,反比例函数y=$\frac{k}{x}$(x>0)的图象经过OA的中点C,交AB于点D.
如图,Rt△ABO的顶点O在坐标原点,点B在x轴上,∠ABO=90°,∠AOB=30°,OB=2$\sqrt{3}$,反比例函数y=$\frac{k}{x}$(x>0)的图象经过OA的中点C,交AB于点D.(1)求反比例函数的关系式;
(2)连接CD,求四边形CDBO的面积.
分析 (1)解直角三角形求得AB,作CE⊥OB于E,根据平行线分线段成比例定理和三角形中位线的性质求得C的坐标,然后根据待定系数法即可求得反比例函数的解析式;
(2)求得D的坐标,进而求得AD的长,得出△ACD的面积,然后根据S四边形CDBO=S△AOB-S△ACD即可求得.
解答 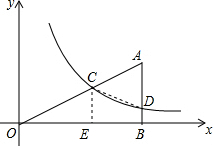 解:(1)∵∠ABO=90°,∠AOB=30°,OB=2$\sqrt{3}$,
解:(1)∵∠ABO=90°,∠AOB=30°,OB=2$\sqrt{3}$,
∴AB=$\frac{\sqrt{3}}{3}$OB=2,
作CE⊥OB于E,
∵∠ABO=90°,
∴CE∥AB,
∴OC=AC,
∴OE=BE=$\frac{1}{2}$OB=$\sqrt{3}$,CE=$\frac{1}{2}$AB=1,
∴C($\sqrt{3}$,1),
∵反比例函数y=$\frac{k}{x}$(x>0)的图象经过OA的中点C,
∴1=$\frac{k}{\sqrt{3}}$,
∴k=$\sqrt{3}$,
∴反比例函数的关系式为y=$\frac{\sqrt{3}}{x}$;
(2)∵OB=2$\sqrt{3}$,
∴D的横坐标为2$\sqrt{3}$,
代入y=$\frac{\sqrt{3}}{x}$得,y=$\frac{1}{2}$,
∴D(2$\sqrt{3}$,$\frac{1}{2}$),
∴BD=$\frac{1}{2}$,
∵AB=2,
∴AD=$\frac{3}{2}$,
∴S△ACD=$\frac{1}{2}$AD•BE=$\frac{1}{2}$×$\frac{3}{2}$×$\sqrt{3}$=$\frac{3\sqrt{3}}{4}$,
∴S四边形CDBO=S△AOB-S△ACD=$\frac{1}{2}$OB•AB-$\frac{3\sqrt{3}}{4}$=$\frac{1}{2}$×2$\sqrt{3}$×2-$\frac{3\sqrt{3}}{4}$=$\frac{5\sqrt{3}}{4}$.
点评 本题考查待定系数法求反比例函数的解析式,解决本题的关键是明确反比例函数图象上点的坐标特征.

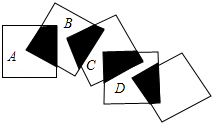 将五个边长都为2cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和是( )cm2.
将五个边长都为2cm的正方形按如图所示摆放,点A、B、C、D分别是四个正方形的中心,则图中四块阴影面积的和是( )cm2.| A. | 2cm2 | B. | 4cm2 | C. | 6cm2 | D. | 8cm2 |
 完成以下证明,并在括号内填写理由:
完成以下证明,并在括号内填写理由: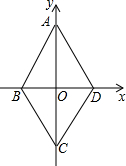 如图,四边形ABCD是周长为20cm的菱形,点A的坐标是(0,4),则点B的坐标为(-3,0).
如图,四边形ABCD是周长为20cm的菱形,点A的坐标是(0,4),则点B的坐标为(-3,0). 一幅长20cm、宽12cm的图案,如图,其中有一横两竖的彩条,横、竖彩条的宽度比为3:2.设竖彩条的宽度为xcm,图案中三条彩条所占面积为ycm2.
一幅长20cm、宽12cm的图案,如图,其中有一横两竖的彩条,横、竖彩条的宽度比为3:2.设竖彩条的宽度为xcm,图案中三条彩条所占面积为ycm2. 如图,将弧长为6π的扇形纸片AOB围成圆锥形纸帽,使扇形的两条半径OA与OB重合(粘连部分忽略不计),则圆锥形纸帽的底面半径是3.
如图,将弧长为6π的扇形纸片AOB围成圆锥形纸帽,使扇形的两条半径OA与OB重合(粘连部分忽略不计),则圆锥形纸帽的底面半径是3.