如图.已知⊙O的直径为8cm.A.B.C三点在⊙O上.且∠ACB=30°.则AB长为( )A．3cmB．4cmC．2$\sqrt{2}$cmD．2$\sqrt{3}$cm 题目和参考答案——青夏教育精英家教网—

题目内容

17．

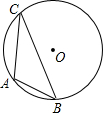如图，已知⊙O的直径为8cm，A、B、C三点在⊙O上，且∠ACB=30°，则AB长为（　　）

A．

3cm

B．

4cm

C．

2$\sqrt{2}$cm

D．

2$\sqrt{3}$cm

分析作直径AD，连接BD，根据圆周角定理得到∠D=∠ACB=30°，根据直角三角形的性质解答即可．

解答解：作直径AD，连接BD，
由圆周角定理得，∠D=∠ACB=30°，
∵AD是⊙O的直径，
∴∠ABD=90°，
∴AB=$\frac{1}{2}$AD=4cm，
故选：B．

点评本题考查的是圆周角定理和直角三角形的性质，掌握同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．半圆（或直径）所对的圆周角是直角，90°的圆周角所对的弦是直径是解题的关键．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

相关题目

6．

完成以下证明，并在括号内填写理由：
已知：如图，∠EAB=∠CDF，CE∥BF．
求证：AB∥CD．
证明：∵CE∥BF已知，
∴∠CDF=∠C两直线平行，内错角相等，
∵∠EAB=∠CDF，
∴∠C=∠EAB，
∴AB∥CD同位角相等，两直线平行．

7．有一列按一定顺序和规律排列的数：
第一个数是$\frac{1}{1×2}$；
第二个数是$\frac{1}{2×3}$；
第三个数是$\frac{1}{3×4}$；
…
对任何正整数n，第n个数与第（n+1）个数的和等于$\frac{2}{n×（n+2）}$．
（1）经过探究，我们发现：$\frac{1}{1×2}=\frac{1}{1}-\frac{1}{2}$，$\frac{1}{2×3}=\frac{1}{2}-\frac{1}{3}$，$\frac{1}{3×4}=\frac{1}{3}-\frac{1}{4}$，
设这列数的第5个数为a，那么$a＞\frac{1}{5}-\frac{1}{6}$，$a=\frac{1}{5}-\frac{1}{6}$，$a＜\frac{1}{5}-\frac{1}{6}$，哪个正确？
请你直接写出正确的结论；
（2）请你观察第1个数、第2个数、第3个数，猜想这列数的第n个数（即用正整数n表示第n数），并且证明你的猜想满足“第n个数与第（n+1）个数的和等于$\frac{2}{n×（n+2）}$”；
（3）设M表示$\frac{1}{1^2}$，$\frac{1}{2^2}$，$\frac{1}{3^2}$，…，$\frac{1}{{{{2016}^2}}}$，这2016个数的和，即$M=\frac{1}{1^2}+\frac{1}{2^2}+\frac{1}{3^2}+…\frac{1}{{{{2016}^2}}}$，
求证：$\frac{2016}{2017}＜M＜\frac{4031}{2016}$．

5．为估计鱼塘中的鱼数，养鱼者首先从鱼塘中打捞了50条鱼，每条鱼做好标记后放回，再从鱼塘中打捞出50条鱼，发现只有1条鱼是有记号的，假设鱼在鱼塘是均匀分布的，则可估计该鱼塘的条数约为2500．

12．一个口袋中有 3 个黑球和若干个白球，在不允许将球倒出来数的前提下，小明为估计其中的白球数，采用了如下的方法：从口袋中随机摸出一球，记下颜色，然后把它放回口袋中，摇匀后再随机摸出一球，记下颜色，…，不断重复上述过程．小明共摸了100次，其中25次摸到黑球．根据上述数据，小明可估计口袋中的白球大约有（　　）

2．在△ABC中，AB=AC，BC=8，当S_△ABC=20时，tanB的值为（　　）

9．为了估计鱼塘青鱼的数量（鱼塘只有青鱼），将200条鲤鱼放进鱼塘，随机捕捞出一条鱼，记下品种后放回，稍后再随机捕捞出一条鱼记下品种，多次重复后发现鲤鱼出现的频率为0.2，那么可以估计鱼塘里青鱼的数量为800条．

6．

如图，将弧长为6π的扇形纸片AOB围成圆锥形纸帽，使扇形的两条半径OA与OB重合（粘连部分忽略不计），则圆锥形纸帽的底面半径是3．

7．

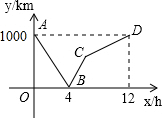一列快车从甲地驶往乙地，一列慢车从乙地驶往甲地，两车同时出发，设慢车行驶的时间为x（h），两车之间的距离为y（km），y与x之间的函数关系如图中折线所示，根据图象得到下列结论，其中正确的是（　　）

	A．	B点表示此时快车到达乙地
	B．	B-C-D段表示慢车先加速后减速最后到达甲地
	C．	快车的速度为166$\frac{2}{3}$km/h
	D．	慢车的速度为125km/h

试题分类