题目内容
9.已知x=$\sqrt{2}$,x=$\sqrt{6}$是关于x的方程x2+ax+b=0的解,求a和b的值.分析 根据根与系数的关系得到$\sqrt{2}$+$\sqrt{6}$=-a,$\sqrt{2}$•$\sqrt{6}$=b,然后根据二次根式的运算求出a和b的值.
解答 解:根据题意得$\sqrt{2}$+$\sqrt{6}$=-a,$\sqrt{2}$•$\sqrt{6}$=b,
所以a=-$\sqrt{2}$-$\sqrt{6}$,b=2$\sqrt{3}$.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
8.已知二次函数y=-x2+6x-8.
(1)该函数图象的对称轴是x=3,顶点坐标(3,1);
(2)选取适当的数据填入下表,并描点画出函数图象;
(3)求抛物线与坐标轴的交点坐标;
(4)利用图象直接回答当x为何值时,函数值y大于0?
(1)该函数图象的对称轴是x=3,顶点坐标(3,1);
(2)选取适当的数据填入下表,并描点画出函数图象;
| x | … | … | |||||
| y | … | … |
(4)利用图象直接回答当x为何值时,函数值y大于0?
 如图所示,一块儿三角形空地ABC,要在其内部建一个菱形花园,使得B为菱形花园的一个顶点,其余3个顶点分别在△ABC的3条边上.你能设计出此菱形花园吗?
如图所示,一块儿三角形空地ABC,要在其内部建一个菱形花园,使得B为菱形花园的一个顶点,其余3个顶点分别在△ABC的3条边上.你能设计出此菱形花园吗?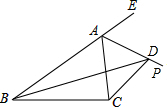 如图,D是△ABC的外角∠CAE平分线AP上一点,求证:DC+DB>AB+AC.
如图,D是△ABC的外角∠CAE平分线AP上一点,求证:DC+DB>AB+AC.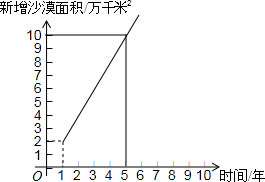 全国每年都有大量土地被沙漠吞没,改造沙漠,保护土地资源己成为一项十分紧迫的任务,某地区现有土地面积100万千米2,沙漠面积200万千米2,土地沙漠化的变化情况如下图所示.
全国每年都有大量土地被沙漠吞没,改造沙漠,保护土地资源己成为一项十分紧迫的任务,某地区现有土地面积100万千米2,沙漠面积200万千米2,土地沙漠化的变化情况如下图所示.