题目内容
20.我们把a,b,c三个数的中位数记作Z{a,b,c},直线y=kx+$\frac{1}{2}$(k>0)与函数y=Z{x2-1,x+1,-x+1}的图象有且只有2个交点,则k的取值为$\frac{1}{2}$<k≤1或k=$\frac{5}{4}$.分析 画出函数y=Z{x2-1,x+1,-x+1}的图象,要使直线y=kx+$\frac{1}{2}$(k>0)与函数y=Z{x2-1,x+1,-x+1}的图象有且只有2个交点,只需直线经过(2,3)和经过(2,$\frac{1}{2}$)之间.
解答 解: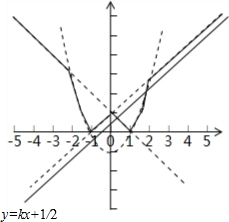 函数y=Z{x2-1,x+1,-x+1}的图象如图所示
函数y=Z{x2-1,x+1,-x+1}的图象如图所示
∵直线y=kx+$\frac{1}{2}$(k>0)与函数y=Z{x2-1,x+1,-x+1}的图象有且只有2个交点,
当直线y=kx+$\frac{1}{2}$(k>0)经过点(2,3)时,则3=2k+$\frac{1}{2}$,
解得k=$\frac{5}{4}$,
当直线y=kx+$\frac{1}{2}$(k>0)经过点(-1,0)时,k=$\frac{1}{2}$,
当k=1时,平行于y=x+1,与函数y=Z{x2-1,x+1,-x+1}的图象也有且仅有两个交点;
∴直线y=kx+$\frac{1}{2}$(k>0)与函数y=Z{x2-1,x+1,-x+1}的图象有且只有2个交点,则k的取值为$\frac{1}{2}$<k≤1或k=$\frac{5}{4}$.
故答案为$\frac{1}{2}$<k≤1或k=$\frac{5}{4}$.
点评 本题考查了一次函数的性质以及中位数的概念,数形结合思想的应用是解题的关键.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
10.在-$\frac{1}{2}$,0,-3,0.5这四个数中,最小的一个数是( )
| A. | -$\frac{1}{2}$ | B. | 0 | C. | -3 | D. | 0.5 |
15.下列说法错误的是( )
| A. | 如果ax=bx,那么a=b | B. | 如果a=b,那么$\frac{a}{{c}^{2}+1}$=$\frac{b}{{c}^{2}+1}$ | ||
| C. | 如果a=b,那么ac-d=bc-d | D. | 如果x=3,那么x2=3x |
 A,B两地间的铁路线长828km,如图是一列慢车和一列快车沿相同路线从A地到B地所行驶的路程y(km)和行驶时间x(h)的变化的图象,根据图象回答下列问题:
A,B两地间的铁路线长828km,如图是一列慢车和一列快车沿相同路线从A地到B地所行驶的路程y(km)和行驶时间x(h)的变化的图象,根据图象回答下列问题: